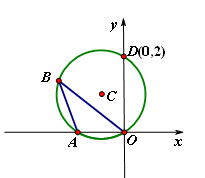
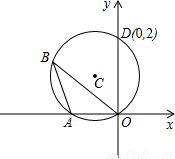
题目内容
 如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知∠OBA=30°,点D的坐标为(0,2),求⊙C半径.
如图,⊙C过原点,与x轴、y轴分别交于A、D两点,已知∠OBA=30°,点D的坐标为(0,2),求⊙C半径.分析:连接AD,则根据90度的圆周角所对的弦是直径,即可证得AD是直径,然后在直角△AOD中,利用三角函数即可求得AD的长,从而求得半径的长.
解答: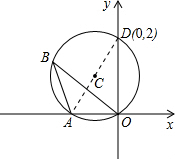 解:连接AD
解:连接AD
∵D(0,2),
∴OD=2.
∵∠DOA=90°,
∴AD为⊙C的直径.
∵∠OBA=∠ADO=30°,
∠DOA=90°,OD=2
∴AD=
.
∴⊙C半径为
.
 解:连接AD
解:连接AD∵D(0,2),
∴OD=2.
∵∠DOA=90°,
∴AD为⊙C的直径.
∵∠OBA=∠ADO=30°,
∠DOA=90°,OD=2
∴AD=
4
| ||
| 3 |
∴⊙C半径为
2
| ||
| 3 |
点评:本题考查了圆周角定理,正确作出辅助线是关键.

练习册系列答案
相关题目
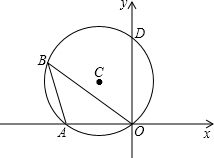 如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是( )
如图,⊙C过原点,与x轴、y轴分别交于A、D两点.已知∠OBA=30°,点D的坐标为(0,2),则⊙C半径是( )A、
| ||||
B、
| ||||
C、4
| ||||
| D、2 |
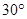 ,点D的坐标为(0,2),求
,点D的坐标为(0,2),求 ⊙C半径。
⊙C半径。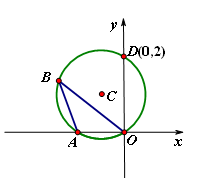
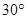 ,点D的坐标为(0,2),求
,点D的坐标为(0,2),求 ⊙C半径。
⊙C半径。