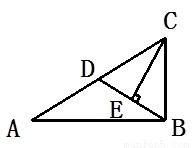题目内容
 16、如图,CE平分∠ACB,且CE⊥DB,∠DAB=∠DBA,又知AC=18,△CDB的周长为28,则BD的长为
16、如图,CE平分∠ACB,且CE⊥DB,∠DAB=∠DBA,又知AC=18,△CDB的周长为28,则BD的长为8
.分析:由已知易得CD=BC,AD=BD,则AC=CD+BD=18,所以BC=28-18=10,则CD=10,即可求得BD.
解答:解:∵CE平分∠ACB,且CE⊥DB,
∴CD=BC,
∵∠DAB=∠DBA,
∴AD=BD,
∵AC=CD+AD=18,
∴AC=CD+BD=18,
∴BC=△BCD的周长-AC=28-18=10,
∴CD=10,
∴BD=18-10=8.
故答案为:8.
∴CD=BC,
∵∠DAB=∠DBA,
∴AD=BD,
∵AC=CD+AD=18,
∴AC=CD+BD=18,
∴BC=△BCD的周长-AC=28-18=10,
∴CD=10,
∴BD=18-10=8.
故答案为:8.
点评:此题主要考查等腰三角形的判定和性质,注意认真观察图中各边之间的关系.

练习册系列答案
相关题目
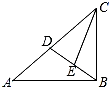 如图,CE平分∠ACB,CE⊥BD于E,若AD=BD,AC=15cm,△CBD的周长为25cm,则BE=
如图,CE平分∠ACB,CE⊥BD于E,若AD=BD,AC=15cm,△CBD的周长为25cm,则BE=