题目内容
如图(a),已知AB是⊙O的直径,CB是⊙O的切线,B为切点,D是⊙O上一点(不A、B重合).
(1)求证:∠DAB=∠DBC;
(2)若AB不是⊙O的直径,其它条件不变,(1)中的结论还成立吗?若成立,则给出你的证明;若不成立,请说明理由.
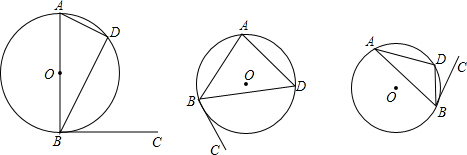
(1)求证:∠DAB=∠DBC;
(2)若AB不是⊙O的直径,其它条件不变,(1)中的结论还成立吗?若成立,则给出你的证明;若不成立,请说明理由.

分析:(1)由AB是⊙O的直径,CB是⊙O的切线,易得∠D=90°,AB⊥BC,然后由同角的余角相等,即可证得:∠DAB=∠DBC;
(2)首先作直径BE,连接DE,同(1),可证得∠BED=∠DBC,又由圆周角定理,可得∠BED=∠DAB,则可证得∠DAB=∠DBC.
(2)首先作直径BE,连接DE,同(1),可证得∠BED=∠DBC,又由圆周角定理,可得∠BED=∠DAB,则可证得∠DAB=∠DBC.
解答:(1)证明:∵AB是⊙O的直径,CB是⊙O的切线,
∴∠D=90°,AB⊥BC,
∴∠DAB+∠ABD=90°,∠ABD+∠DBC=90°,
∴∠DAB=∠DBC;
 (2)成立.
(2)成立.
理由:如图2,作直径BE,连接DE,
∵BE是⊙O的直径,CB是⊙O的切线,
∴∠BDE=90°,BE⊥BC,
∴∠BED+∠EBD=90°,∠EBD+∠DBC=90°,
∴∠BED=∠DBC,
∵∠BED=∠DAB,
∴∠DAB=∠DBC;
如图3,作直径BE,连接DE,
∵BE是⊙O的直径,CB是⊙O的切线,
∴∠BDE=90°,BE⊥BC,
∴∠BED+∠EBD=90°,∠EBD+∠DBC=90°,
∴∠BED=∠DBC,
∵∠BED=∠DAB,
∴∠DAB=∠DBC.
∴∠D=90°,AB⊥BC,
∴∠DAB+∠ABD=90°,∠ABD+∠DBC=90°,
∴∠DAB=∠DBC;
 (2)成立.
(2)成立.理由:如图2,作直径BE,连接DE,
∵BE是⊙O的直径,CB是⊙O的切线,
∴∠BDE=90°,BE⊥BC,
∴∠BED+∠EBD=90°,∠EBD+∠DBC=90°,
∴∠BED=∠DBC,
∵∠BED=∠DAB,
∴∠DAB=∠DBC;
如图3,作直径BE,连接DE,
∵BE是⊙O的直径,CB是⊙O的切线,
∴∠BDE=90°,BE⊥BC,
∴∠BED+∠EBD=90°,∠EBD+∠DBC=90°,
∴∠BED=∠DBC,
∵∠BED=∠DAB,
∴∠DAB=∠DBC.
点评:此题考查了切线的性质以及圆周角定理.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
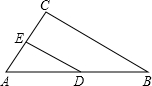 如图,△ABC中,已知AB=8,BC=6,CA=4,DE是中位线,则DE=( )
如图,△ABC中,已知AB=8,BC=6,CA=4,DE是中位线,则DE=( )| A、4 | B、3 | C、2 | D、1 |
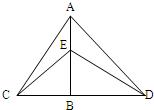 18、如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
18、如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形: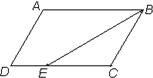 15、如图,?ABCD中,已知AB=9cm,AD=6cm,BE平分∠ABC交DC边于点E,则DE等于( )
15、如图,?ABCD中,已知AB=9cm,AD=6cm,BE平分∠ABC交DC边于点E,则DE等于( ) 2、如图,△ABC中,已知AB=AC=x,BC=6,则腰长x的取值范围是( )
2、如图,△ABC中,已知AB=AC=x,BC=6,则腰长x的取值范围是( )
