题目内容
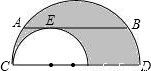
 如图两个半圆内切于点C,大圆的弦AB切小圆与F,且AB平行于大半圆的直径CD,若AB=4cm,则两个半圆所夹的阴影部分的面积为
如图两个半圆内切于点C,大圆的弦AB切小圆与F,且AB平行于大半圆的直径CD,若AB=4cm,则两个半圆所夹的阴影部分的面积为分析:设大圆、小圆半径分别是R、r厘米. 连接OA、OB、O1E,则OA=OB=R,O1E=r 作OF垂直于AB于F点,则OF垂直平分AB,
再根据勾股定理可求出R2-r2的值,利用阴影部分面积=
-
即可求出答案.
再根据勾股定理可求出R2-r2的值,利用阴影部分面积=
| πR2 |
| 2 |
| πr2 |
| 2 |
解答:解:设大圆、小圆半径分别是R、r厘米. 连接OA、OB、O1E,
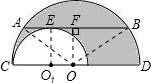
则OA=OB=R,O1E=r
作OF垂直于AB于E点,则OF垂直平分AB,
∵AB是小圆的切线,
∴OF∥O1 E,
又∵AB∥CD
∴OF=O1E=r
又∵OA2=OF2+AF2=OF2+(
)2,
即R2=r2+4,R2-r2=4,
∴阴影部分面积=
-
,
=π
,
=2π.
故答案为:2π.

则OA=OB=R,O1E=r
作OF垂直于AB于E点,则OF垂直平分AB,
∵AB是小圆的切线,
∴OF∥O1 E,
又∵AB∥CD
∴OF=O1E=r
又∵OA2=OF2+AF2=OF2+(
| AB |
| 2 |
即R2=r2+4,R2-r2=4,
∴阴影部分面积=
| πR2 |
| 2 |
| πr2 |
| 2 |
=π
| R2-r2 |
| 2 |
=2π.
故答案为:2π.
点评:本题考查的是垂径定理、勾股定理及切线的性质,设出两圆的半径,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
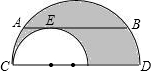 如图两个半圆内切于点C,大圆的弦AB切小圆与F,且AB平行于大半圆的直径CD,若AB=4cm,则两个半圆所夹的阴影部分的面积为________cm2.
如图两个半圆内切于点C,大圆的弦AB切小圆与F,且AB平行于大半圆的直径CD,若AB=4cm,则两个半圆所夹的阴影部分的面积为________cm2.