题目内容
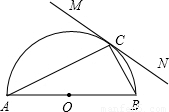
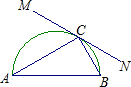如图，已知直线MN与以AB为直径的半圆相切于点C，在MN上是否存在点D，使AB•CD=AC•BC（ ）| A、不存在 | B、存在一点 | C、存在二点 | D、存在无数点 |
分析：存在两个点D，使AB•CD=AC•BC成立，要证明乘积的形式通常可以转化为比例的形式：①
=
，此时需证Rt△ABC∽Rt△ACD，那么过A作MN的垂线，那么垂足即为符合条件的D点；②
=
，此时需证Rt△ABC∽Rt△CBD，则过B作MN的垂线，垂足也符合D点的条件．两者的证明过程一致，都是通过弦切角得出一组对应角相等，再加上一组直角得出三角形相似．
| AB |
| AC |
| BC |
| CD |
| AB |
| BC |
| AC |
| CD |
解答：解：存在符合条件的点D，使AB•CD=AC•BC，
证明：①过A作AD⊥MN于D，则AB•CD=AC•BC
证明：∵MN是半圆的切线，且切点为C，
∴∠ACD=∠B，
∵AB为半圆的直径，又AD⊥MN，
∴∠ADC=∠ACB=90°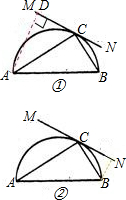
∴△ABC∽△ACD，
∴
=
，即AB•CD=AC•BC；
②过B作BD⊥MN于D，则AB•CD=AC•BC，
证明：∵MN是半圆的切线，且切点为C，
∴∠BCD=∠A，
∵AB为半圆的直径，又BD⊥MN，
∴∠BDC=∠ACB=90°，
∴△ABC∽△CBD，
∴
=
，即AB•CD=AC•BC，
因此MN上存在两个点D，使AB•CD=AC•BC．
故选C
证明：①过A作AD⊥MN于D，则AB•CD=AC•BC
证明：∵MN是半圆的切线，且切点为C，
∴∠ACD=∠B，
∵AB为半圆的直径，又AD⊥MN，
∴∠ADC=∠ACB=90°
∴△ABC∽△ACD，
∴
| AB |
| BC |
| AC |
| CD |
②过B作BD⊥MN于D，则AB•CD=AC•BC，
证明：∵MN是半圆的切线，且切点为C，
∴∠BCD=∠A，
∵AB为半圆的直径，又BD⊥MN，
∴∠BDC=∠ACB=90°，
∴△ABC∽△CBD，
∴
| AB |
| AC |
| CB |
| CD |
因此MN上存在两个点D，使AB•CD=AC•BC．
故选C
点评：本题考查了圆周角定理，弦切角定理及相似三角形的判定和性质，其中弦切角定理为：圆的弦切角等于夹弧所对的圆周角．要求学生能够熟练掌握相似的判断和性质并应用，考查了分类讨论及数形结合的思想，培养了学生分析问题，解决问题的能力．
练习册系列答案
相关题目
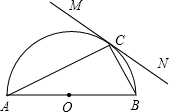如图，已知直线MN与以AB为直径的半圆相切于点C，∠A=28°．
如图，已知直线MN与以AB为直径的半圆相切于点C，∠A=28°．