题目内容
如果△ABC的两边长分别为a、b,那么△ABC的面积不可能等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由于是任意三角形,故需用含三角函数的式子表示三角形的面积,即S△ABC=
absinC,那么当∠C=90°时,△ABC的面积最大,且最大值是
ab,再结合完全平方公式(a-b)2≥0,可得
ab≤
(a2+b2),
再结合每一个选项,通过计算即可判断.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
再结合每一个选项,通过计算即可判断.
解答: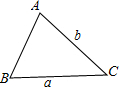 解:∵△ABC的两边长时a、b,
解:∵△ABC的两边长时a、b,
∴S△ABC=
absinC,
当∠C=90°时,△ABC的面积最大,且S△ABC=
ab,
又∵(a-b)2≥0,
即
ab≤
(a2+b2),
A、∵S=
(a2+b2),
故此选项可能;
B、∵
(a2+b2)>
(a2+b2),
故此选项不可能;
C、∵
(a+b)2=
[
(a2+b2)+
ab]≥
ab,
故此选项可能;
D、∵
ab<
ab,
故此选项可能.
故选B.
 解:∵△ABC的两边长时a、b,
解:∵△ABC的两边长时a、b,∴S△ABC=
| 1 |
| 2 |
当∠C=90°时,△ABC的面积最大,且S△ABC=
| 1 |
| 2 |
又∵(a-b)2≥0,
即
| 1 |
| 2 |
| 1 |
| 4 |
A、∵S=
| 1 |
| 4 |
故此选项可能;
B、∵
| 1 |
| 2 |
| 1 |
| 4 |
故此选项不可能;
C、∵
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
故此选项可能;
D、∵
| 1 |
| 4 |
| 1 |
| 2 |
故此选项可能.
故选B.
点评:本题考查了三角形面积公式、三角形函数值、完全平方公式、不等式的计算.解答此题的关键是用含三角函数值的式子表示三角形的面积.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (a2+b2)
(a2+b2) (a2+b2)
(a2+b2) (a+b)2
(a+b)2