题目内容
随着人民的生活水平的不断提高,学生身边的零用钱也多了.夏雪同学调查了班级同学身上有多少零用钱,将每位同学的零用钱记录下来,下面是全班40名同学的零用钱的数目(单位:元)
2,5,0,5,2,5,6,5,0,5,5,5,2,5,8,0,5,5,2,5,
5,8,6,5,2,5,5,2,5,6,5,5,0,6,5,6,5,2,5,0.
(1)请你写出同学的零用钱(0元,2元,5元,6元8元)出现的频数;
(2)求出同学的零用钱的平均数、中位数和众数;
(3)假如老师随机问一个同学的零用钱,老师最有可能得到的回答是多少元?
解:(1)0元的频数是5,2元的频数是7,5元的频数是21,6元的频数是5,8元的频数是2;
(2)平均数是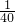 (2×7+5×21+6×5+8×2)=4.125,
(2×7+5×21+6×5+8×2)=4.125,
将数据从小到大排列,找第20、21人的数值,均为5,故中位数是5;5的数目最多,故众数是5;
(3)因为“5元”的频数最大,即其频率最大;故老师最有可能得到的回答是5元.
分析:(1)频数即为该组数据出现的次数,仔细观察后找到该数据出现的次数即为该组数据的频数.
(2)根据平均数、中位数和众数的计算方法,进行计算可得答案;
(3)因为“5元”的频数最大,即其频率最大,故最有可能得到的回答是5元.
点评:本题考查了频率、频数、中位数、众数、平均数的定义.各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率= .
.
(2)平均数是
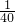 (2×7+5×21+6×5+8×2)=4.125,
(2×7+5×21+6×5+8×2)=4.125,将数据从小到大排列,找第20、21人的数值,均为5,故中位数是5;5的数目最多,故众数是5;
(3)因为“5元”的频数最大,即其频率最大;故老师最有可能得到的回答是5元.
分析:(1)频数即为该组数据出现的次数,仔细观察后找到该数据出现的次数即为该组数据的频数.
(2)根据平均数、中位数和众数的计算方法,进行计算可得答案;
(3)因为“5元”的频数最大,即其频率最大,故最有可能得到的回答是5元.
点评:本题考查了频率、频数、中位数、众数、平均数的定义.各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率=
 .
. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目