题目内容
如图△ABC中,D为BC边上一点,且△ABD与△ADC面积相等,则线段AD一定是
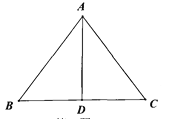
A. △ABC的高 B. △ABC的中线
C. △ABC的角平分线 D. 以上选项都不对
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
题目内容
如图△ABC中,D为BC边上一点,且△ABD与△ADC面积相等,则线段AD一定是

A. △ABC的高 B. △ABC的中线
C. △ABC的角平分线 D. 以上选项都不对
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案