题目内容
数学活动小组接受学校的一项任务:在紧靠围墙的空地上,利用围墙及一段长为60米的木栅栏围成一块生物园地,请设计一个方案使生物园的面积尽可能大.活动小组提交如图的方案.设靠墙的一边长为x米,则不靠墙的一边长为(60-2x)米,面积y=(60-2x)x2.当x=15时,y最大值=450m2;机灵的小明想:如果改变生物园的形状,围成的面积会更大吗?请你帮小明设计两个方案,要求画出图形,算出面积大小;并找出面积最大的方案.
【答案】分析:根据周长相同时讨论面积的大小问题可借鉴割圆术的思路,将四边形靠墙两边向外移,因为可利用围墙,所以围成半圆形面积最大.
解答:
解:(1)围成腰与上底相等的等腰梯形,如图所示,则腰长是20米,面积:
S= ×(20+40)×10
×(20+40)×10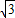 =300
=300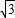 >450;
>450;
(2)围成半圆形,如图所示.则周长是60米,
面积S= π•(
π•(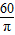 )2=
)2=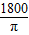 >450.
>450.
点评:此题属于设计性题目,可以利用割圆术的思想,当周长一定时,圆的面积最大来设计方案.
解答:

解:(1)围成腰与上底相等的等腰梯形,如图所示,则腰长是20米,面积:
S=
 ×(20+40)×10
×(20+40)×10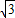 =300
=300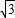 >450;
>450;(2)围成半圆形,如图所示.则周长是60米,
面积S=
 π•(
π•(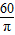 )2=
)2=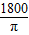 >450.
>450.点评:此题属于设计性题目,可以利用割圆术的思想,当周长一定时,圆的面积最大来设计方案.

练习册系列答案
相关题目




