题目内容
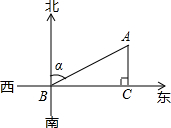
一艘船向东匀速航行，上午9时到达B处，看到有一灯塔在它的北偏东60°，距离为80海里的A处（即图中∠α=60°，AB=80海里），上午11时到达C处，看到灯塔在它的正北方向．
（1）求BC的长（精确到0.1海里）；
（2）这艘船航行的速度（精确到1海里/时）．
解：在Rt△ABC中，∵BC=AB×COS30°
≈69.3
∵船从B到C行驶了两个小时，
∴这艘船航行的速度为35海里/时
答：船航行的速度为35海里/时．
分析：利用直角三角形性质边角关系，BC=AB×cos30°求出BC，然后除以船从B到C所用时间即可．
点评：本题考查了直角三角形的性质，利用边与角的关系求解即可．
≈69.3
∵船从B到C行驶了两个小时，
∴这艘船航行的速度为35海里/时
答：船航行的速度为35海里/时．
分析：利用直角三角形性质边角关系，BC=AB×cos30°求出BC，然后除以船从B到C所用时间即可．
点评：本题考查了直角三角形的性质，利用边与角的关系求解即可．
练习册系列答案
相关题目
24、一艘船向东匀速航行，上午9时到达B处，看到有一灯塔在它的北偏东60°，距离为80海里的A处（即图中∠α=60°，AB=80海里），上午11时到达C处，看到灯塔在它的正北方向．
一艘船向正东匀速航行到O处时，看到有一灯塔在它的北偏东60°且距离为32
