题目内容
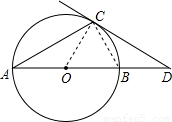
（2000•福建）如图，AB是⊙O的直径，点D在AB的延长线上，BD=OB，CD与⊙O切于C，那么∠CAB= 度．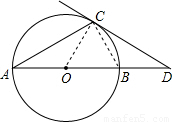
【答案】分析：连接OC，BC．则OC⊥CD，∠ACB=90°．由BD=OB可证△OBC是等边三角形，得解．
解答：解：连接OC，BC．
∵CD是切线，
∴OC⊥CD．
∵BD=OB，
∴BC=OB=OC．
∴∠ABC=60°．
∵AB是直径，
∴∠ACB=90°，
∴∠CAB=30°．
点评：此题考查了切线的性质及直角三角形的性质，难度不大．
解答：解：连接OC，BC．
∵CD是切线，
∴OC⊥CD．
∵BD=OB，
∴BC=OB=OC．
∴∠ABC=60°．
∵AB是直径，
∴∠ACB=90°，
∴∠CAB=30°．
点评：此题考查了切线的性质及直角三角形的性质，难度不大．
练习册系列答案
相关题目
