题目内容
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的 .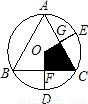
【答案】分析:首先连接OG,根据垂径定理的知识,易证得Rt△OCG≌Rt△OCF,设OG=a,根据直角三角形的性质与等边三角形的知识,即可求得阴影部分四边形OFCG的面积与△ABC的面积,继而求得答案.
解答: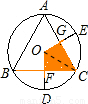 解:连接OC,
解:连接OC,
∵AB=BC=CA,
∴∠ACB=60°,
∵OD⊥BC,OE⊥AC,
∴CG= AC,CF=
AC,CF= BC,
BC,
∴CG=CF,
∵OC=OC,
∴Rt△OCG≌Rt△OCF,
∴∠ACO=∠BCO=30°,
∴OG= OC,
OC,
设OG=a,OC=2a,CG=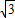 a,
a,
∴S△ABC= BC•
BC•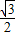 BC=
BC= ×2
×2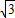 a×
a×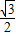 ×2
×2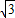 a=3
a=3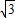 a2,
a2,
S四边形CGOF=S△OCG+S△OCF=2S△OCG=2× ×a×
×a×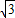 a=
a=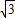 a2,
a2,
∴阴影部分四边形OFCG的面积是△ABC的面积的 .
.
故答案为: .
.
点评:此题考查了垂径定理,等边三角形的性质,直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.
解答:
 解:连接OC,
解:连接OC,∵AB=BC=CA,
∴∠ACB=60°,
∵OD⊥BC,OE⊥AC,
∴CG=
 AC,CF=
AC,CF= BC,
BC,∴CG=CF,
∵OC=OC,
∴Rt△OCG≌Rt△OCF,
∴∠ACO=∠BCO=30°,
∴OG=
 OC,
OC,设OG=a,OC=2a,CG=
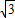 a,
a,∴S△ABC=
 BC•
BC•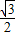 BC=
BC= ×2
×2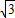 a×
a×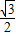 ×2
×2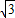 a=3
a=3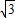 a2,
a2,S四边形CGOF=S△OCG+S△OCF=2S△OCG=2×
 ×a×
×a×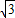 a=
a=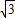 a2,
a2,∴阴影部分四边形OFCG的面积是△ABC的面积的
 .
.故答案为:
 .
.点评:此题考查了垂径定理,等边三角形的性质,直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
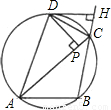
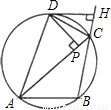
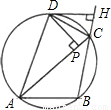
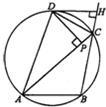 7、如图,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BH,垂足是H,下列结论:①CH=CP;②AD=DB;③AP=BH;④DH为圆的切线.其中一定成立的是( )
7、如图,圆内接△ABC的外角∠ACH的平分线与圆交于D点,DP⊥AC,垂足是P,DH⊥BH,垂足是H,下列结论:①CH=CP;②AD=DB;③AP=BH;④DH为圆的切线.其中一定成立的是( ) 如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的
如图,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,阴影部分四边形OFCG的面积是△ABC的面积的