题目内容
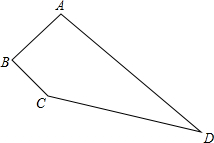
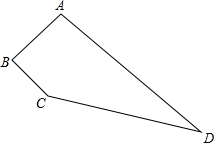 如下图,在四边形ABCD中,∠B=90°,AB=8,BC=6,CD=24,AD=26,求四边形ABCD的面积.
如下图,在四边形ABCD中,∠B=90°,AB=8,BC=6,CD=24,AD=26,求四边形ABCD的面积.
分析:连接AC,根据已知条件运用勾股定理逆定理可证△ABC和△ACD为直角三角形,然后代入三角形面积公式将两直角三角形的面积求出来,两者面积相加即为四边形ABCD的面积.
解答: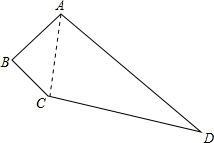 解:连接AC,
解:连接AC,
∵∠B=90°,
∴△ABC为直角三角形,
∵AC2=AB2+BC2=82+62=102,
∵AC>0,
∴AC=10,
在△ACD中,
∵AC2+CD2=100+576=676,AD2=262=676,
∴AC2+CD2=AD2,
∴△ACD为直角三角形,且∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD=
×6×8+
×10×24=144.
 解:连接AC,
解:连接AC,∵∠B=90°,
∴△ABC为直角三角形,
∵AC2=AB2+BC2=82+62=102,
∵AC>0,
∴AC=10,
在△ACD中,
∵AC2+CD2=100+576=676,AD2=262=676,
∴AC2+CD2=AD2,
∴△ACD为直角三角形,且∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
点评:通过作辅助线可将一般的四边形转化为两个直角三角形,使面积的求解过程变得简单.

练习册系列答案
相关题目
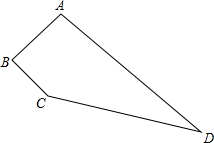 如下图,在四边形ABCD中,∠B=90°,AB=8,BC=6,CD=24,AD=26,求四边形ABCD的面积.
如下图,在四边形ABCD中,∠B=90°,AB=8,BC=6,CD=24,AD=26,求四边形ABCD的面积.