题目内容
【题目】已知扇形OAB的半径为r,C为![]() 上的任一点(不与A、B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN.
上的任一点(不与A、B重合),CM⊥OA,垂足为M,CN⊥OB,垂足为N,连接MN.
(1)如图①,∠AOB=90°,求证MN=r;
(2)如图②,∠AOB=45°,探索MN与r的数量关系.

【答案】(1)证明见解析(2)![]() r
r
【解析】试题分析: ![]() 连接OC,四边形OMCN是矩形,即可得证.
连接OC,四边形OMCN是矩形,即可得证.
![]() 以O为圆心,OA为半径画⊙O,证明MN是△CPQ的中位线,即可得出结果.
以O为圆心,OA为半径画⊙O,证明MN是△CPQ的中位线,即可得出结果.
试题解析: ![]() 证明:连接OC,
证明:连接OC,
∵CM⊥OA, CN⊥OB,
∴∠CMO=∠CNO=90°,
又∠AOB=90°,
∴四边形OMCN是矩形.
∴MN=OC=r .

![]() 以O为圆心,OA为半径画⊙O,
以O为圆心,OA为半径画⊙O,
延长CM,CN分别与⊙O交于点P,Q,连接OP,OQ ,PQ,OC
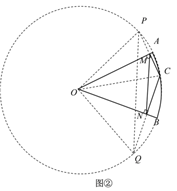
∵OA⊥PC,∴PA=AC, ![]()
同理CN=NQ, ![]()
∴∠POA=∠COA,∠QOB=∠COB,
∴∠POQ=2∠AOB=90°,
在△CPQ中,MN是△CPQ的中位线,
![]() .
.
在Rt△OPQ中
![]()
![]()

练习册系列答案
相关题目
