题目内容
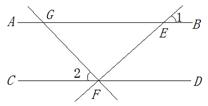
为了决定谁将获得仅有的一张科普报告入场券,甲和乙设计了如下的一个游戏:口袋中有编号分别为1、2、3的红球三个和编号为4的白球一个,四个球除了颜色或编号不同外,没有任何别的区别,摸球之前将小球搅匀,摸球的人都蒙上眼睛.先甲无放回摸两次,每次摸出一个球;再把甲摸出的两个球同时放回口袋后,乙再摸,乙只摸一个球.如果甲摸出的两个球都是红色,甲得1分,否则,甲得0分;如果乙摸出的球是白色,乙得1分,否则,乙得0分 ;得分高的获得入场券,如果得分相同,游戏重来.
(1)(4分)运用列表或画树状图求甲得1分的概率;
(2)(4分)这个游戏是否公平?请说明理由.
(1) (2)不公平,理由(见解析).
(2)不公平,理由(见解析).
解析试题分析:(1)运用列表或画树状图求甲得1分的概率.(2)根据列表或画树状图分别求得P(乙得1分)= ,P(甲得1分)≠P(乙得1分),比较即可得不公平.
,P(甲得1分)≠P(乙得1分),比较即可得不公平.
试题解析:(1)列表或树状图如下
1 2 3 4 1 1分 1分 0分 2 1分 1分 0分 3 1分 1分 0分 4 0分 0分 0分 
P(甲得1分)=
(2)不公平.
∵P(乙得1分)=
∴P(甲得1分)≠P(乙得1分)
∴不公平
考点:列举法求概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与反比例函数
与反比例函数 的图象交于点
的图象交于点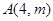 和
和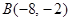 ,与
,与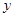 轴交于点
轴交于点 .(1)
.(1)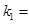 ,
,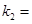 ;
;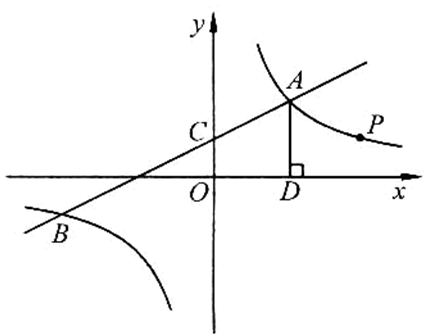
 时,
时,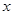 的取值范围是 ;
的取值范围是 ; 作
作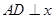 轴于点
轴于点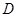 ,点
,点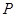 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线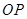 与线段
与线段 交于点
交于点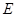 ,当
,当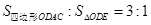 时,求点
时,求点 与反比例函数
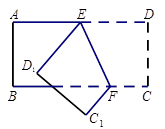
与反比例函数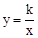 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将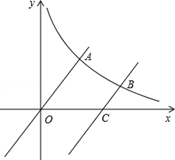
 ,求反比例函数的解析式.
,求反比例函数的解析式. 的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.
的图象与一次函数y=mx+b的图象交于A(1,3),B(n,﹣1)两点.