题目内容
 如图,以坐标原点为圆心作圆交y轴与点E,AB为⊙O的弦,且AB∥x轴,交y轴于点D,双曲线y=
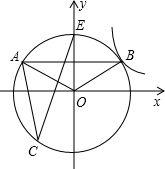
如图,以坐标原点为圆心作圆交y轴与点E,AB为⊙O的弦,且AB∥x轴,交y轴于点D,双曲线y= 经过点B,C为⊙O上的一点,若∠ACE=30°,ED=2时,则k=________.
经过点B,C为⊙O上的一点,若∠ACE=30°,ED=2时,则k=________.
4
分析:连接BE、BF,根据圆的对称性,可得则 =
= ,∠BFE=30°,解直角三角形可得出BD、DF的长度,继而得出点B的坐标,将点B的坐标代入可得出k的值.
,∠BFE=30°,解直角三角形可得出BD、DF的长度,继而得出点B的坐标,将点B的坐标代入可得出k的值.
解答:

连接BE、BF,则 =
= ,
,
从而∠ACE=∠BFE=30°,
∵EF是直径,
∴∠EBF=90°,
∴∠EBD=30°,
∵ED=2,
∴BD=2 ,
,
∴DF=6,
则圆的直径EF=ED+DF=8,半径EO=4,DO=EO-ED=2,
故可得点B的坐标为(2 ,2),
,2),
将点B的坐标代入得:2= ,
,
解得:k=4 .
.
故答案为:4 .
.
点评:本题属于反比例函数的综合题,涉及了待定系数法求函数解析式、圆周角定理及解直角三角形的知识,解答本题的关键是熟练各个知识点,并将各知识点融会贯通.

分析:连接BE、BF,根据圆的对称性,可得则
 =
= ,∠BFE=30°,解直角三角形可得出BD、DF的长度,继而得出点B的坐标,将点B的坐标代入可得出k的值.
,∠BFE=30°,解直角三角形可得出BD、DF的长度,继而得出点B的坐标,将点B的坐标代入可得出k的值.解答:

连接BE、BF,则
 =
= ,
,从而∠ACE=∠BFE=30°,
∵EF是直径,
∴∠EBF=90°,
∴∠EBD=30°,
∵ED=2,
∴BD=2
 ,
,∴DF=6,
则圆的直径EF=ED+DF=8,半径EO=4,DO=EO-ED=2,
故可得点B的坐标为(2
 ,2),
,2),将点B的坐标代入得:2=
 ,
,解得:k=4
 .
.故答案为:4
 .
.点评:本题属于反比例函数的综合题,涉及了待定系数法求函数解析式、圆周角定理及解直角三角形的知识,解答本题的关键是熟练各个知识点,并将各知识点融会贯通.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
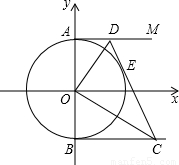
 切线AM上一点(D与A不重合),DE切⊙O于点E,与BN交于点C,且AD<BC.设AD=m,BC=n.
切线AM上一点(D与A不重合),DE切⊙O于点E,与BN交于点C,且AD<BC.设AD=m,BC=n. (2012•宜昌二模)如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
(2012•宜昌二模)如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )