题目内容
【题目】已知:关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0
(1)求证:方程有两个实数根;
(2)当k为何值时,此方程的两个实数根互为相反数;
(3)我们定义:若一元二次方程ax2+bx+c=0的两个正实数根x1、x2(x1>x2),满足2<![]() <3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
<3,则称这个一元二次方程有两个“梦想根”.如果关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,求k的范围.
【答案】(1)证明见解析(2)1(3)﹣![]() <k<-
<k<-![]() 或﹣3<k<﹣2
或﹣3<k<﹣2
【解析】
试题分析:(1)根据方程的判别式,可得答案;
(2)根据互为相反数的和为零,可得关于k的方程,根据解方程,可得答案;
(3)根据方程的梦想根,可得不等式组,根据解不等式组,可得答案.
试题解析:(1)关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0,
a=k,b=﹣(k﹣1),c=﹣1,
△=b2﹣4ac=[﹣(k﹣1)]2﹣4k(﹣1)=k2+2k+1=(k+1)2≥0,
关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个实数根;
(2)关于x的一元二次方程kx2﹣(k﹣1)x﹣1=0,
x1=![]() ,x2=
,x2=![]() ,
,
方程的两个实数根互为相反数,得
x1+x2=![]() +
+![]() =0,
=0,
即![]() =0,
=0,
解得k=1,
当k=1时,此方程的两个实数根互为相反数;
(3)当k>0时,x1=1,x2=﹣![]() <0,不符合题意;
<0,不符合题意;
当﹣1≤k<0时,x1=﹣![]() ,x2=1,2<
,x2=1,2<![]() <3,得
<3,得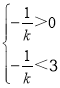 ,
,
解得﹣![]() <k<-
<k<-![]() ;
;
当k<﹣1时,x1=﹣![]() ,x2=1,由2<
,x2=1,由2<![]() <3,得2<﹣k<3,
<3,得2<﹣k<3,
解得﹣3<k<﹣2不符合题意舍去,
综上所述:于x的一元二次方程kx2﹣(k﹣1)x﹣1=0有两个“梦想根”,k的范围是:
﹣![]() <k<-
<k<-![]() 或﹣3<k<﹣2.
或﹣3<k<﹣2.

练习册系列答案
相关题目