Question

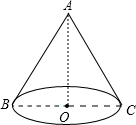如图，圆锥的侧面积为15π，底面半径为3，则圆锥的高AO为

 

．

Answer 1

分析：要求圆锥的高，关键是求出圆锥的母线长，即圆锥侧面展开图中的扇形的半径．已知圆锥的底面半径就可求得底面圆的周长，即扇形的弧长，已知扇形的面积和弧长就可求出扇形的半径，即圆锥的高．

解答：解：由题意知：展开图扇形的弧长是2×3π=6π，
设母线长为L，则有

1

2

×6πL=15π，
∴L=5，
由于母线，高，底面半径正好组成直角三角形，
∴在直角△AOC中高AO=

AC2-OC2

=4．
故本题答案为：4．

点评：圆锥的侧展开图是扇形，此题考查了圆锥体的侧面展开图的计算，揭示了平面图形与立体图形之间的关系．