题目内容
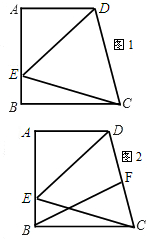 如图1所示,在直角梯形ABCD中,AD∥BC,∠DCB=75°,AB⊥BC,以CD为一边的等边△DCE的另一顶点E在腰AB上.
如图1所示,在直角梯形ABCD中,AD∥BC,∠DCB=75°,AB⊥BC,以CD为一边的等边△DCE的另一顶点E在腰AB上.(1)求∠AED的度数;
(2)求证:AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30°,△BFC的面积=4cm2,求AB的长度.
分析:(1)根据直角梯形ABCD,得到∠DCB+∠ADC=180°,∠BAD=∠B=90°,求出∠ADC=105°,根据等边三角形的性质得出∠EDC=∠DCE=60°,求出∠EDA=45°即可;
(2)连接AC,由∠EDA=∠ADE=45°,得到AE=AD,根据等边三角形,得到CE=CD证△DCA≌△DCA,推出∠ECA=∠DCA=30°,求出∠CAB=45°,推出∠CAB=∠ACB即可;
(3)作FG⊥BC于G,由∠DCB=75°,∠CBF=30°,推出∠DCB=∠BFC,得到BC=BF,根据三角形的面积公式得到
BC×FG=4,求出BC=4,即可得出答案.
(2)连接AC,由∠EDA=∠ADE=45°,得到AE=AD,根据等边三角形,得到CE=CD证△DCA≌△DCA,推出∠ECA=∠DCA=30°,求出∠CAB=45°,推出∠CAB=∠ACB即可;
(3)作FG⊥BC于G,由∠DCB=75°,∠CBF=30°,推出∠DCB=∠BFC,得到BC=BF,根据三角形的面积公式得到
| 1 |
| 2 |
解答:解:(1)∵在直角梯形ABCD中,AD∥BC,
∴∠DCB+∠ADC=180°,∠BAD=∠B=90°,
∵∠DCB=75°,
∴∠ADC=105°,
∵△DCE是等边三角形,
∴∠EDC=∠DCE=60°,
∴∠EDA=45°,
∴∠AED=45°,
答:∠AED的度数是45°;
(2)证明:连接AC,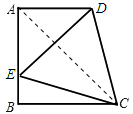
∵∠AED=∠ADE=45°,
∴AE=AD
∵△DCE是等边三角形,
∴CE=CD
∵AC=AC,
∴△DCA≌△ECA,
∴∠ECA=∠DCA=30°,
∵∠DCB=75°,
∴∠ACB=45°
∵∠B=90°,
∴∠CAB=45°,
∴∠CAB=∠ACB,
∴AB=BC;
(3)解:作FG⊥BC于G,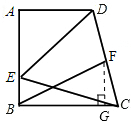
∵∠DCB=75°,∠CBF=30°,
∴∠BFC=75°,
∴∠DCB=∠BFC,
∴BC=BF,
在Rt△BFG中,∠CBF=30°,
∴BF=2FG=BC,
∵
BC×FG=4,
∴
BC2=4cm2,
∴BC=4cm,
∴AB=BC=4cm,
即AB长为4cm.
答:AB的长度是4cm.
∴∠DCB+∠ADC=180°,∠BAD=∠B=90°,
∵∠DCB=75°,
∴∠ADC=105°,
∵△DCE是等边三角形,
∴∠EDC=∠DCE=60°,
∴∠EDA=45°,
∴∠AED=45°,
答:∠AED的度数是45°;
(2)证明:连接AC,

∵∠AED=∠ADE=45°,
∴AE=AD
∵△DCE是等边三角形,
∴CE=CD
∵AC=AC,
∴△DCA≌△ECA,
∴∠ECA=∠DCA=30°,
∵∠DCB=75°,
∴∠ACB=45°
∵∠B=90°,
∴∠CAB=45°,
∴∠CAB=∠ACB,
∴AB=BC;
(3)解:作FG⊥BC于G,

∵∠DCB=75°,∠CBF=30°,
∴∠BFC=75°,
∴∠DCB=∠BFC,
∴BC=BF,
在Rt△BFG中,∠CBF=30°,
∴BF=2FG=BC,
∵
| 1 |
| 2 |
∴
| 1 |
| 4 |
∴BC=4cm,
∴AB=BC=4cm,
即AB长为4cm.
答:AB的长度是4cm.
点评:本题主要考查对直角梯形,全等三角形的性质和判定,等边三角形的性质和判定,等腰三角形的性质和判定,三角形的面积,含30度角的直角三角形的性质等知识点的理解和掌握,能综合运用这些性质进行证明是解此题的关键,题型较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
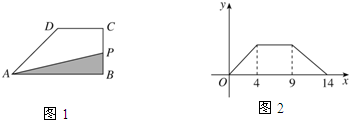
 .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为 
 .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为(
)
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为(
) 