题目内容
【题目】如图所示是反比例函数![]() 与正比例函数
与正比例函数![]() 的图象,点
的图象,点![]() 与点
与点![]() 均在反比例函数的图象上,点
均在反比例函数的图象上,点![]() 在直线
在直线![]() 上,点
上,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点,四边形
的对称点,四边形![]() 是平行四边形.
是平行四边形.
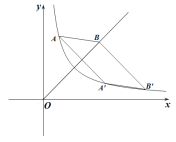
(1)试说明点![]() 在反比例函数图象上;
在反比例函数图象上;
(2)设点![]() 的横坐标为
的横坐标为![]() ,试用
,试用![]() 表示出点
表示出点![]() 的坐标并求出
的坐标并求出![]() 的值.
的值.
【答案】(1)、证明过程见解析;(2)、B′(m+3,m-3);m=![]()
【解析】
试题分析:(1)、首先根据点A的坐标求出k的值,然后得出点A′的坐标,看这个点坐标是否满足函数解析式;(2)、首先得出点B的坐标,根据平行四边形的性质得出点B′的坐标,然后进行求解.
试题解析:(1)、∵A(1,4)在y=![]() 上,∴k=1×4=4,
上,∴k=1×4=4,
∵点A′是点A关于直线y=x的对称点,
∴点A′为(4,1),
当x=4时,代入y=![]() 中,y=1,
中,y=1,
∴点A′(4,1)在反比例函数图象上;
(2)、∵点B在直线y=x上,又点B的横坐标为m,
∴点B的坐标为(m,m) ,
∵四边形AA′B′B是平行四边形, ∴AA′与BB′平行且相等,
∴B′可由B(m,m)沿AA′方向平移而得,
由点的坐标的平移规律,可知点B′的坐标为(m+3,m-3),
∵点B′在反比例函数的图象上,
∴(m+3)(m-3)=4,
解得m=±![]() ,
,
∵m>0,
∴m=![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
【题目】某校把学生的纸笔测试、实践能力、成长记录三项成绩分别按50%,20%,30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩如下表(单位:分),学期总评成绩优秀的是( )
纸笔测试 | 实践能力 | 成长记录 | |
甲 | 90 | 83 | 95 |
乙 | 88 | 90 | 95 |
丙 | 90 | 88 | 90 |
A.甲B.乙、丙C.甲、乙D.甲、丙