题目内容
甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.

(1 )A、B两地的距离 千米;乙车速度是 ;a表示 .
(2)乙出发多长时间后两车相距330千米?

(1 )A、B两地的距离 千米;乙车速度是 ;a表示 .
(2)乙出发多长时间后两车相距330千米?
解:(1)560; 100;甲车到达B地时甲乙两车之间的距离为a千米。
(2)设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,
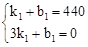 ,解得:
,解得: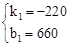 。
。
∴直线BC的解析式为S=﹣220t+660。
当﹣220t+660=330时,解得t=1.5,
∴t﹣1=1.5﹣1=0.5。
∵相遇后甲车到达B地的时间为:(3﹣1)×100÷120= 小时,
小时,
∴点D的横坐标为 +3=
+3= ,a=(120+100)×
,a=(120+100)× =
= 千米。
千米。
∴D( ,
, )。
)。
设直线CD的解析式为S=k2t+b2(k2≠0),
将C(3,0),D( ,
, )代入得,
)代入得,
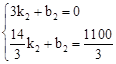 ,解得:
,解得: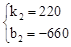 。
。
∴直线CD的解析式为S=220t﹣660。
当220t﹣660=330时,解得t=4.5。
∴t﹣1=4.5﹣1=3.5。
答:乙出发多长0.5小时或3.5小时后两车相距330千米。
(2)设直线BC的解析式为S=k1t+b1(k1≠0),
将B(1,440),C(3,0)代入得,
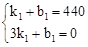 ,解得:
,解得: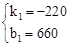 。
。∴直线BC的解析式为S=﹣220t+660。
当﹣220t+660=330时,解得t=1.5,
∴t﹣1=1.5﹣1=0.5。
∵相遇后甲车到达B地的时间为:(3﹣1)×100÷120=
 小时,
小时,∴点D的横坐标为
 +3=
+3= ,a=(120+100)×
,a=(120+100)× =
= 千米。
千米。∴D(
 ,
, )。
)。设直线CD的解析式为S=k2t+b2(k2≠0),
将C(3,0),D(
 ,
, )代入得,
)代入得,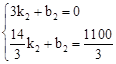 ,解得:
,解得: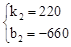 。
。∴直线CD的解析式为S=220t﹣660。
当220t﹣660=330时,解得t=4.5。
∴t﹣1=4.5﹣1=3.5。
答:乙出发多长0.5小时或3.5小时后两车相距330千米。
试题分析:(1)根据图象,甲出发时的S值即为A、B两地间的距离;先求出甲车的速度,然后设乙车的速度为xkm/h,再利用相遇问题列出方程求解即可;然后求出相遇后甲车到达B地的时间,再根据路程=速度×时间求出两车的相距距离a即可:
∵t=0时,S=560,∴A、B两地的距离为560千米。
甲车的速度为:(560﹣440)÷1=120千米/小时,
设乙车的速度为x千米/小时,则(120+x)×(3﹣1)=440,解得x=100。
∴A、B两地的距离为560千米,乙车的速度为100千米/小时,a表示甲车到达B地时甲乙两车之间的距离为a千米。
(2)设直线BC的解析式为S=k1t+b1(k1≠0),利用待定系数法求出直线BC的解析式,再令S=330,求出t的值,减去1即为相遇前乙车出发的时间;设直线CD的解析式为S=k2t+b2(k2≠0),利用待定系数法求出直线CD的解析式,再令S=330,求出t的值,减去1即为相遇后乙车出发的时间。

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 向上平移m个单位后,与直线
向上平移m个单位后,与直线 的交点在第一象限,则m的取值范围是
的交点在第一象限,则m的取值范围是




 上一点,则点B与其对应点B′间的距离为
上一点,则点B与其对应点B′间的距离为

