题目内容
己知两个任意正数a和b,有下列命题:(1)若a+b=2,则
| ab |
(2)若a+b=
| 1 |
| 2 |
| ab |
| 1 |
| 4 |
(3)若a+b=
| 2 |
| ab |
| ||
| 2 |
| ab |
分析:先根据所给的条件推出相应的结论,再找出a+b与
的关系即可.
| ||
| 2 |
解答:解:(1)若a+b=2,则
≤1,有2>
;
(2)若a+b=
,则
≤
,有
>
×
=
;
(3)若a+b=
,则
≤
,有
>
×
=
;
∴得到a+b≥
.
| ab |
| 1 |
| 2 |
(2)若a+b=
| 1 |
| 2 |
| ab |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(3)若a+b=
| 2 |
| ab |
| ||
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
∴得到a+b≥
| ||
| 2 |
点评:本题是找规律题,找到a+b≥
是解题的关键.
| ||
| 2 |

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
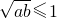
 ,则
,则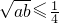
 ,则
,则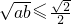 ;根据以上三个命题所提供的规律,试猜想出a+b与
;根据以上三个命题所提供的规律,试猜想出a+b与 应满足的最佳关系式:______.
应满足的最佳关系式:______.
 ,则
,则
 ,则
,则 ;根据以上三个命题所提供的规律,试猜想出a+b与
;根据以上三个命题所提供的规律,试猜想出a+b与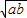 应满足的最佳关系式: .
应满足的最佳关系式: .