Question

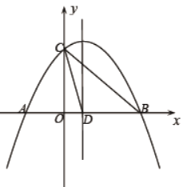
【题目】已知，如图，点P是平行四边形ABCD外一点，PE∥AB交BC于点E．PA、PD分别交BC于点M、N，点M是BE的中点．

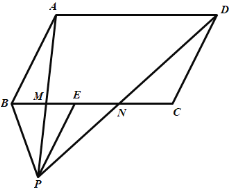
（1）求证：CN=EN；

（2）若平行四边形ABCD的面积为12，求△PMN的面积．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

（1）根据平行线的性质得到∠BAM=∠EPM，根据线段中点的定义得到BM=EM，根据全等三角形的性质得到AB=PE，根据平行四边形的判定和性质定理即可得到结论；
（2）过P作PH⊥AD于H，交BC于G，根据全等三角形的性质得到AM=PM，根据平行线等分线段定理得到AG=HG=PH，根据平行四边形和三角形的面积公式即可得到结论．

解：（1）连接DE,PC.

∵PE∥AB，
∴∠BAM=∠EPM，
∵∠AMB=∠PME，
∵点M是BE的中点，
∴BM=EM，
∴△ABM≌△PEM（AAS），
∴AB=PE，
∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD，

∴PE∥CD，PE=CD，
∴四边形PEDC是平行四边形，
∴EN=CN；
（2）过P作PH⊥AD于H，交BC于G，
由（1）知，△ABM≌△PEM，
∴AM=PM，
∵AD∥BC，
∴AG=HG=PH，
∵BM=EM，EN=CN，
∴MN=BC=AD，
∵平行四边形ABCD的面积为12，

∴ADPH=24，
∴△PMN的面积=MNPG=×AD×PH=ADPH=×24=3．