题目内容
【题目】如图,△ABC中,∠A=90°,AB=AC,顶点B为(﹣4,0),顶点C为(1,0),将△ABC关于y轴轴对称变换得到△A1B1C1,再将△A1B1C1关于直线x=2(即过(2,0)垂直于x轴的直线)轴对称变换得到△A2B2C2,再将△A2B2C2关于直线x=4轴对称变换得到△A3B3C3,再将△A3B3C3关于直线x=6轴对称变换得到△A4B4C4…,按此规律继续变换下去,则点A10的坐标为_____.
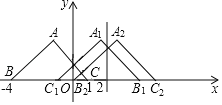
【答案】(15.5,2.5)
【解析】
根据对称性质可得点的坐标变化规律,由此即可求解.
解:△ABC中,∠A=90°,AB=AC,
顶点B为(﹣4,0),顶点C为(1,0),
∴BC=5
∴A(﹣1.5,2.5)
将△ABC关于y轴轴对称变换得到△A1B1C1,
∴A1 (1.5,2.5)
再将△A1B1C1关于直线x=2轴对称变换得到△A2B2C2,
∴A2 (2.5,2.5)
再将△A2B2C2关于直线x=4轴对称变换得到△A3B3C3,
∴A3 (5.5,2.5)
再将△A3B3C3关于直线x=6轴对称变换得到△A4B4C4,
∴A4 (6.5,2.5)
…
按此规律继续变换下去,
A5 (8.5,2.5),
A6 (9.5,2.5),
A7 (11.5,2.5)
则点A10的坐标为(15.5,2.5),
故答案为:(15.5,2.5).

练习册系列答案
相关题目