Question

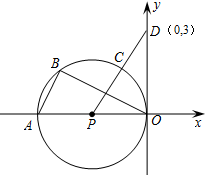（2012•凉山州）如图，已知直径为OA的⊙P与x轴交于O、A两点，点B、C把

OA

三等分，连接PC并延长PC交y轴于点D（0，3）．
（1）求证：△POD≌△ABO；
（3）若直线l：y=kx+b经过圆心P和D，求直线l的解析式．

Answer 1

分析：（1）首先连接PB，由直径为OA的⊙P与x轴交于O、A两点，点B、C把

OA

三等分，可求得∠APB=∠DPO=60°，∠ABO=∠POD=90°，即可得△PAB是等边三角形，可得AB=OP，然后由ASA，即可判定：△POD≌△ABO；
（2）易求得∠PDO=30°，由OP=OD•tan30°，即可求得点P的坐标，然后利用待定系数法，即可求得直线l的解析式．

解答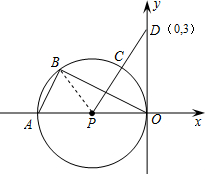：（1）证明：连接PB，
∵直径为OA的⊙P与x轴交于O、A两点，点B、C把

OA

三等分，
∴∠APB=∠DPO=

1

3

×180°=60°，∠ABO=∠POD=90°，
∵PA=PB，
∴△PAB是等边三角形，
∴AB=PA，∠BAO=60°，
∴AB=OP，∠BAO=∠OPD，
在△POD和△ABO中，

∠OPD=∠BAO OP=BA ∠POD=∠ABO

∴△POD≌△ABO（ASA）；

（2）解：由（1）得△POD≌△ABO，
∴∠PDO=∠AOB，
∵∠AOB=

1

2

∠APB=

1

2

×60°=30°，
∴∠PDO=30°，
∴OP=OD•tan30°=3×

3

3

=

3

，
∴点P的坐标为：（-

3

，0）
∴

b=3 - 3 k+b=0

，
解得：

k= 3 b=3

，
∴直线l的解析式为：y=

3

x+3．

点评：此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式．此题综合性较强，难度适中，注意准确作出辅助线，注意数形结合思想的应用．