题目内容
 如图是反比例函数y=
如图是反比例函数y=| k | x |
(1)比例系数k的值是
12
12
;(2)写出该图象的另一个分支上的2个点的坐标:
(-2,-6)
(-2,-6)
、(-3,-4)等
(-3,-4)等
;(3)当x在什么范围取值时,y是小于3的正数?
(4)如果自变量x取值范围为2≤x≤3,求y的取值范围.
分析:(1)根据图象过点(2,6),即可得出k的值;
(2)根据(1)中所求解析式,即可得出图象上点的坐标;
(3)根据y=
<3求出x的取值范围即可;
(4)根据当x=2时,y=6,当x=3时,y=4,得出y的取值范围即可.
(2)根据(1)中所求解析式,即可得出图象上点的坐标;
(3)根据y=
| 12 |
| x |
(4)根据当x=2时,y=6,当x=3时,y=4,得出y的取值范围即可.
解答:解:(1)∵图象过点(2,6),
∴k=xy=12;
故答案为:12;
(2)(-2,-6),(-3,-4)答案不确定;
故答案为:(-2,-6),(-3,-4)等;
(3)当y=
<3时,则x>4;
(4)当x=2时,y=6,当x=3时,y=4,
故2≤x≤3时,则4≤y≤6.
∴k=xy=12;
故答案为:12;
(2)(-2,-6),(-3,-4)答案不确定;
故答案为:(-2,-6),(-3,-4)等;
(3)当y=
| 12 |
| x |
(4)当x=2时,y=6,当x=3时,y=4,
故2≤x≤3时,则4≤y≤6.
点评:此题主要考查了待定系数法求反比例函数解析式以及不等式解法等知识,根据不等式的性质得出x与y的取值范围是解题关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
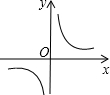 如图是反比例函数
如图是反比例函数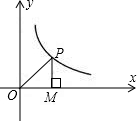 如图是反比例函数
如图是反比例函数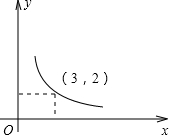 我们知道函数的表示方法有三种,如图是反比例函数的其中一种表示方法,请写出函数的另两种表示方法的名称,并分别用这两种表示方法表示此函数.
我们知道函数的表示方法有三种,如图是反比例函数的其中一种表示方法,请写出函数的另两种表示方法的名称,并分别用这两种表示方法表示此函数.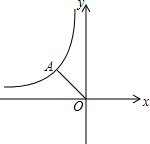 如图是反比例函数y=
如图是反比例函数y=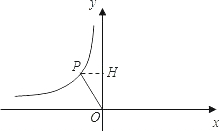 如图是反比例函数
如图是反比例函数