题目内容
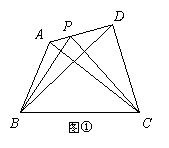
提出问题:如图①,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?
探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
 (1)当AP=
(1)当AP=![]() AD时(如图②):
AD时(如图②):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD .
S△ABD .
∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
 ∴S△CDP=
∴S△CDP=![]() S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
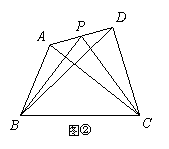
(2)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
(3)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________________;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为:________________;
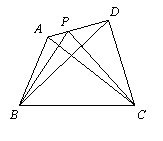
(4)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
问题解决:当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为:___________.
解:⑵ ∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
 ∴S△ABP=
∴S△ABP=![]() S△ABD .
S△ABD .
又∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
∴S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
⑶ S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC ;
S△ABC ;
⑷ S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC ;
S△ABC ;
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD .
S△ABD .
又∵PD=AD-AP=![]() AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=![]() S△CDA .
S△CDA .
∴S△PBC =S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-![]() S△ABD-
S△ABD-![]() S△CDA
S△CDA
=S四边形ABCD-![]() (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-![]() (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
∴S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .
问题解决: S△PBC=![]() S△DBC+
S△DBC+![]() S△ABC .
S△ABC .

 画出示意图,写出你提出的问题,并直接写出结论,不必证明.
画出示意图,写出你提出的问题,并直接写出结论,不必证明.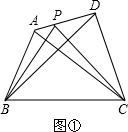
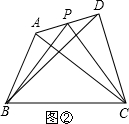




 AD时(如图2):
AD时(如图2):  AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等, 
 ,
, ,
,



 ;
; AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程; AD时,S△PBC与S△ABC和S△DBC之间的关系式为:______;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为:______; AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系,写出求解过程; 时,S△PBC与S△ABC和S△DBC之间的关系式为:________。
时,S△PBC与S△ABC和S△DBC之间的关系式为:________。