Question

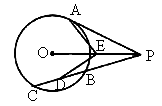
如图所示，已知PA切⊙O于点A，割线PBC交⊙O于B、C，PD⊥AB于D，PD、AO的延长线交于点E，连结CE并延长交⊙O于点F，连结AF．

(1)求证：△PBD∽△PEC；

(2)若AB＝12，tan∠EAF=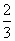，求⊙O的半径的长．

Answer 1

答案：
解析：

(1)提示：可证△PAD∽△PEA．得PA2＝PD·PE又由切割线定理，有PA2＝PB·PC，则PD·PE＝PB·PC由于∠CPE公共，则△PBD∽△PEC;(2)连BF，可证BF为直径，利用相似比和三角函数求AF＝18，后由勾股定理求得R＝3．