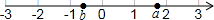题目内容
有理数a，b，c在数轴上的位置如图，则化简|a+c|+|b+c|+|c-1|+|a-2c|-|b-c|的结果是（ ）
| A．2a-c | B．1 | C．-1 | D．c-2a+1 |
由图可知：|a+c|=a+c，|b+c|=-b-c，|c-1|=1-c，|a-2c|=2c-a，|b-c|=c-b，
∴原式=（a+c）+（-b+c）+（1-c）+（2c-a）-（c-b）=1．
故选B．
∴原式=（a+c）+（-b+c）+（1-c）+（2c-a）-（c-b）=1．
故选B．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
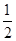和0.2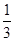
和―0.333
