题目内容
(2007•雅安)如图,在Rt△ABC中,∠ACB为90°,CD⊥AB,cos∠BCD= ,BD=1,则边AB的长是( )
,BD=1,则边AB的长是( )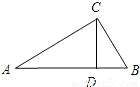
A.

B.

C.2
D.

【答案】分析:在直角三角形中解题,根据角的余弦值与三角形边的关系及勾股定理求出三角形的边长.
解答:解:∵cos∠BCD= ,则设CD=2x,BC=3x,
,则设CD=2x,BC=3x,
根据勾股定理得,12+(2x)2=(3x)2,
∴x=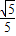 .
.
由于∠BCD=∠BAC,
所以设AC=2y,AB=3y,根据勾股定理得,
(3y)2-(2y)2=(3× )2-y=
)2-y= AB=
AB= ×3=
×3= .
.
故选D.
点评:图中的三个三角形两两相似,于是∠CAD的余弦就是∠BCD的余弦,据此结合根据勾股定理解答.
解答:解:∵cos∠BCD=
 ,则设CD=2x,BC=3x,
,则设CD=2x,BC=3x,根据勾股定理得,12+(2x)2=(3x)2,
∴x=
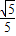 .
.由于∠BCD=∠BAC,
所以设AC=2y,AB=3y,根据勾股定理得,
(3y)2-(2y)2=(3×
 )2-y=
)2-y= AB=
AB= ×3=
×3= .
.故选D.
点评:图中的三个三角形两两相似,于是∠CAD的余弦就是∠BCD的余弦,据此结合根据勾股定理解答.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目