题目内容
【题目】如图所示,矩形OABC的邻边OA、OC分别与x、y轴重合,矩形OABC的对称中心P(4,3),点Q由O向A以每秒1个单位速度运动,点M由C向B以每秒2个单位速度运动,点N由B向C以每秒2个单位速度运动,设运动时间为t秒,三点同时出发,当一点到达终点时同时停止.
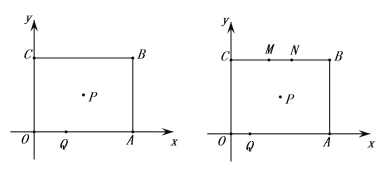
(1)根据题意,可得点B坐标为__________,AC=_________;
(2)求点Q运动几秒时,△PCQ周长最小?
(3)在点M、N、Q的运动过程中,能否使以点O、Q、M、N为顶点的四边形是平行四边形?若能,请求出t值;若不能,请说明理由.
【答案】(1)10 (2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)根据四边形OABC为矩形,矩形OABC的对称中心P(4,3),即可得到B的坐标,再结合勾股定理可得AC的长.
(2)首先根据题意可得△PCQ周长等于CP、CQ、PQ的线段之和,而CP是定值,进而只要CQ和PQ的和最小即可.
(3)假设能,设出t值,利用MN=OQ,计算出t值即可.
(1)根据四边形OABC为矩形,矩形OABC的对称中心P(4,3)
可得B点的坐标为(8,6)
根据勾股定理可得![]()
(2)设点Q运动t秒时,△PCQ周长最小
根据题意可得![]()
![]()
要使△PCQ周长最小,则必须CQ+PQ最短,过x轴作P点的对称点P’

所以可得C、P’、Q在一条直线上
![]() C(0,6),
C(0,6),![]() (4,-3)
(4,-3)
设直线方程为![]()
![]() 即
即
因此![]() ,C所在的直线为
,C所在的直线为![]()
所以Q点的坐标为(![]() ,0)
,0)
所以OQ=![]()
因此t=![]()
(3)根据题意要使点O、Q、M、N为顶点的四边形是平行四边形
则OQ=MN
OQ=t
MN=8-2t-2t=8-4t或MN=2t+2t-8=4t-8
所以t=8-4t或t=4t-8
所以可得t=![]() 或t=
或t=![]()

练习册系列答案
相关题目