题目内容
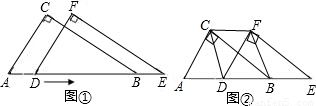
某同学用两个完全相同的直角三角尺重叠在一起(如图①)固定△ABC不动,将△DEF沿线段AB向右平移.(1)若∠A=60°,斜边AB=4,设AD=x,两个直角三角尺重叠部分的面积为y,试求出y与x的函数关系式,并写出自变量的取值范围;
(2)当D移至到什么位置时.四边形CDBF是菱形,并加以证明;
(3)当D移至AB中点时(如图②),四边形CDBF能否为正方形?若能,请你说明理由;若不能,请你添加一个条件说明四边形CDBF为正方形?

分析:(1)根据平移的性质得到DF∥AC,所以由平行线的性质、勾股定理求得GD=
,BG=
=
,所以由三角形的面积公式列出函数关系式;
(2)当D移至AB的中点时,四边形CDBF是菱形.根据“直角三角形斜边上的中线等于斜边的一半”推知
CD=
AB,BF=
DE.所以AD=CD=BD=CF,又由BE=AD,则CD=BD=BF=CF,故四边形CDBF是菱形;
(3)不能为正方形,添加条件:AC=BC时,四边形CDBF为正方形.根据有一内角为直角的菱形是正方形来添加条件.
| 4-x |
| 2 |
| BD2-DG2 |
| ||
| 2 |
(2)当D移至AB的中点时,四边形CDBF是菱形.根据“直角三角形斜边上的中线等于斜边的一半”推知
CD=
| 1 |
| 2 |
| 1 |
| 2 |
(3)不能为正方形,添加条件:AC=BC时,四边形CDBF为正方形.根据有一内角为直角的菱形是正方形来添加条件.
解答: 解(1)如图①∵DF∥AC,
解(1)如图①∵DF∥AC,
∴∠DGB=∠C=90°,∠GDB=∠A=60°,∠GBD=30°
∵BC=4-x,
∴GD=
,BG=
=
y=S△BDG=
×
×
=
(O≤x≤4);
(2)当D移至AB的中点时,四边形CDBF是菱形.
证明:∵∠ACB=∠DFE=90°,D是AB的中点
∴CD=
AB,EF=
DE
∴CD=BD=BF=BE
∵CF=BD
∴CD=BD=BF=CF
∴四边形CDBF是菱形;
(3)不能为正方形,添加条件:AC=BC时,四边形CDBF为正方形.
证明:∵AC=BC,D是AB的中点.
∴CD⊥AB即∠CDB=90°
∵四边形CDBF为菱形,
∴四边形CDBF是正方形.
 解(1)如图①∵DF∥AC,
解(1)如图①∵DF∥AC,∴∠DGB=∠C=90°,∠GDB=∠A=60°,∠GBD=30°
∵BC=4-x,
∴GD=
| 4-x |
| 2 |
| BD2-DG2 |
| ||
| 2 |
y=S△BDG=
| 1 |
| 2 |
| 4-x |
| 2 |
| ||
| 2 |
| ||
| 8 |
(2)当D移至AB的中点时,四边形CDBF是菱形.
证明:∵∠ACB=∠DFE=90°,D是AB的中点
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD=BD=BF=BE
∵CF=BD
∴CD=BD=BF=CF
∴四边形CDBF是菱形;
(3)不能为正方形,添加条件:AC=BC时,四边形CDBF为正方形.
证明:∵AC=BC,D是AB的中点.
∴CD⊥AB即∠CDB=90°
∵四边形CDBF为菱形,
∴四边形CDBF是正方形.
点评:本题是几何变换综合题型,主要考查了平移变换的性质,勾股定理,正方形的判定,菱形的判定与性质以及直角三角形斜边上的中线.(2)难度稍大,根据三角形斜边上的中线推知CD=BD=BF=BE是解题的关键.

练习册系列答案
相关题目
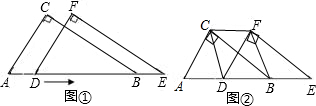 某同学用两个完全相同有一个角为60°的直角三角尺重叠在一起(如图)固定△ABC不动,将△DEF沿线段AB向右平移,当D移至AB中点时(如图②).
某同学用两个完全相同有一个角为60°的直角三角尺重叠在一起(如图)固定△ABC不动,将△DEF沿线段AB向右平移,当D移至AB中点时(如图②). ,若和为奇数,则甲同学去参赛,否则乙同学去参赛.
,若和为奇数,则甲同学去参赛,否则乙同学去参赛.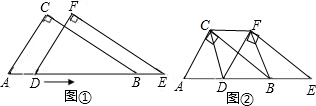 某同学用两个完全相同有一个角为60°的直角三角尺重叠在一起(如图)固定△ABC不动,将△DEF沿线段AB向右平移,当D移至AB中点时(如图②).
某同学用两个完全相同有一个角为60°的直角三角尺重叠在一起(如图)固定△ABC不动,将△DEF沿线段AB向右平移,当D移至AB中点时(如图②).