题目内容
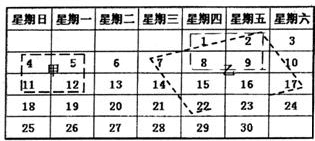
如图是2007年11月份的日历牌,我们在日历牌中用两种不同的方式选择四个数.
(1)从甲中选择构成的“矩形”中发现:11×5-12×4=7,即对角线上两数积的差为7.请你平移矩形甲,使它的四个顶点落在其他的四个数上,对角线上的两数积的差还为7吗?
(2)对乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,你又能得出什么结论?
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例:如果你认为具有一般性,请假设所选择的某个数为n,然后通过含n的代数式的运算加以说明.

(1)从甲中选择构成的“矩形”中发现:11×5-12×4=7,即对角线上两数积的差为7.请你平移矩形甲,使它的四个顶点落在其他的四个数上,对角线上的两数积的差还为7吗?
(2)对乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,你又能得出什么结论?
(3)由第(1)(2)小题得出的这些规律是否具有一般性?如果你认为不具有一般性,请举反例:如果你认为具有一般性,请假设所选择的某个数为n,然后通过含n的代数式的运算加以说明.
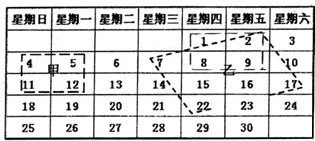
分析:(1)平移矩形甲,使它的四个顶点落在其他四个数上,对角线的两数积的差还是7,例如8×2-1×9=7;
(2)乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,其对角线的两数积之差为-75,例如22×2-7×17=-75;
(3)因为日历上的数据排列规律为左右相邻的数相差1,图中上下交叉的两个数相差6和8,根据整式的运算可得.
(2)乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,其对角线的两数积之差为-75,例如22×2-7×17=-75;
(3)因为日历上的数据排列规律为左右相邻的数相差1,图中上下交叉的两个数相差6和8,根据整式的运算可得.
解答:解:(1)平移矩形甲,使它的四个顶点落在其他的四个数上,对角线的两数积的差还为7,例如:8×2-1×9=7;
(2)例如:22×2-7×17=-75,将平行四边形向下平移一个数,得到29×9-14×24=-75,所以乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,得到对角线的两数积之差为-75;
(3)证明:设最小的一个数为n,则
(n+1)(n+7)-n(n+8)=n2+8n+7-n2-8n=7.
即甲中选择构成的“矩形”顶点处的四个数字,按上述方法计算和平移,其对角线的两数积之差为7;
设最小的一个数为n,则
n(n+20)-(n+5)(n+15)=n2+20n-n2-20n-75=-75.
即乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,其对角线的两数积之差为-75.
(2)例如:22×2-7×17=-75,将平行四边形向下平移一个数,得到29×9-14×24=-75,所以乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,得到对角线的两数积之差为-75;
(3)证明:设最小的一个数为n,则
(n+1)(n+7)-n(n+8)=n2+8n+7-n2-8n=7.
即甲中选择构成的“矩形”顶点处的四个数字,按上述方法计算和平移,其对角线的两数积之差为7;
设最小的一个数为n,则
n(n+20)-(n+5)(n+15)=n2+20n-n2-20n-75=-75.
即乙中选择构成的“平行四边形”顶点处的四个数字,按上述方法计算和平移,其对角线的两数积之差为-75.
点评:本题通过日历考查了规律型:数字的变化.列代数式的关键是正确理解文字语言中的关键词,找到其中的数量关系列出式子.要熟悉日历上的数据排列规律为左右相邻的数相差1,上下相邻的两个数相差7.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
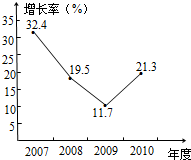 如图是近年来我国年财政收入同比(与上一年比较)增长率的折线统计图,其中2008年我国财政收入约为61330亿元.下列命题:
如图是近年来我国年财政收入同比(与上一年比较)增长率的折线统计图,其中2008年我国财政收入约为61330亿元.下列命题: