Question

(本题10分）

已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y = 的图像上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限.

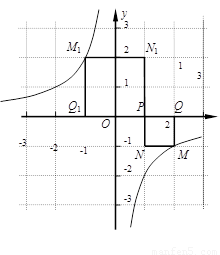
（1）如图所示，若反比例函数解析式为y= ，P点坐标为（1， 0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标；

（温馨提示：作图时，别忘了用黑色字迹的钢笔或签字笔描黑喔！）

M1的坐标是     ▲     

（2） 请你通过改变P点坐标，对直线M1 M的解析式y﹦kx＋b进行探究可得 k﹦  ▲  ，    若点P的坐标为（m，0）时，则b﹦  ▲   ；

（3） 依据(2)的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标．

 

Answer 1

【答案】

 

（1）（－1，2）

（2）-1 ， m

（3）M1，M的坐标分别为（，），（，）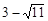

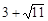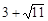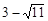【解析】解：（1）如图；M1 的坐标为（－1，2）  ……2分

   （2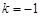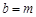）， …………………4分（各2分）

   （3）由（2）知，直线M1 M的解析式为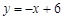

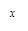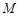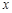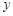        则(，)满足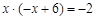

        解得 ，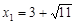

        ∴  ，

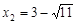
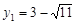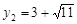
     ∴M1，M的坐标分别为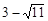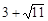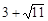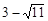（，），（，）．……………4分