题目内容

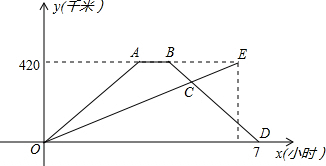快车与慢车分别从相距420千米的甲乙两地同时相向出发，匀速而行，快车到达乙地后停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地．快慢两车距各自出发地的路程y（千米）与所用的时间x（时）的关系如图所示，下列说法正确的有（　　）
①快车返回的速度为140千米/时；   
②慢车的速度为70千米/时；   
③出发
14
3
小时时，快慢两车距各自出发地的路程相等；
④快慢两车出发
9
7
小时时相距150千米．
A、1个B、2个C、3个D、4个
练习册系列答案
相关题目
若点A（-2，m）在正比例函数y=-
1
2
x的图象上，则m的值是（　　）
A、
1
4
B、-
1
4
C、1
D、-1
如图所示，一次函数y=ax+b与x轴的交点为A（2，0），交y轴于B（0，1），那么不等式ax+b＜0的解集为（　　）
A、x＞1B、x＜1C、x＞2D、x＜2
如图1，在同一直线上，甲自点A开始追赶匀速前进的乙，且图2表示两人之间的距离与所经过时间的函数关系．若乙的速度为1.5m/s，则经过40s，甲自点A移动了（　　）
A、60mB、61.8mC、67.2mD、69m
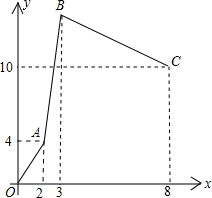某仓库有甲乙丙三辆运货车，每辆车只负责进货和出货，丙车每小时的运输量最多，乙车每小时的运输量最少，乙车每小时运6吨，甲、乙、丙三辆运输车开始工作后，仓库的库存量y（吨）与工作时间x（小时）之间的函数图象如图所示，其中OA段只有甲、丙两车参与运输，AB段只有乙、丙两车参与运输，BC段只有甲、乙两车参与运输．下列说法：
①甲车是出货车；
②丙车是进货车；
③甲车每小时运货8吨；
④工作3小时仓库的库存量为20吨，
其中正确的有（　　）
A、1个B、2个C、3个D、4个
如图，在平面角坐标系中，已知点A、B分别在△OCD的边OC、OD上，且A、B、C三点的坐标分别为（2，3）、（2，1）、（4，6）．若AB∥CD，过点P（2，m）的射线OP交直线CD于点Q，则点Q的纵坐标为（　　）
A、mB、2mC、-mD、-2m
下列运算正确的是（　　）
A、a2•a3=a6
B、-2（a-b）=-2a-2b
C、2x2+3x2=5x4
D、（-
1
2
）-2=4
下列计算中正确的是（　　）
A、
1
3
+
1
2
=
2
5
B、
3-27
=3
C、a6=（a3）2
D、b-2=-b2
计算（-2a1+xb2）3=-8a9b6，则x的值是（　　）
A、0B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网