题目内容
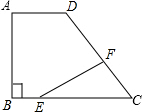 已知:如图,在直角梯形ABCD中,AD∥BC,∠A=90°,BC=CD=10,sinC=
已知:如图,在直角梯形ABCD中,AD∥BC,∠A=90°,BC=CD=10,sinC=| 4 | 5 |
(1)求直角梯形ABCD的面积;
(2)点E是BC上一点,过点E作EF⊥DC于点F.求证:AB•CE=EF•CD.
分析:(1)如图,过点D作DG⊥BC于点G,这样把梯形分割成直角三角形和矩形,然后解直角△DGC,求出DG、CG,这样就可以求出梯形的面积了;
(2)根据(1)的结论和已知容易证明DGC∽△EFC,这样就可以证明AB•CE=EF•CD了.
(2)根据(1)的结论和已知容易证明DGC∽△EFC,这样就可以证明AB•CE=EF•CD了.
解答:(1)解:过点D作DG⊥BC于点G,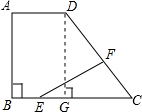
∵AD∥BC,
∴四边形ABGD是矩形.
∴AB=DG,AD=BG.
在△CDG中,∠DGC=90°,CD=BC=10,
sinC=
,DG=8,CG=6,
∴AD=BG=4.
∴AD+BC=14.
∴梯形ABCD的面积S=56.
(2)证明:∵DG⊥BC,EF⊥DC,
∴∠DGC=∠EFC=90°.
又∵∠C=∠C,
∴△DGC∽△EFC.
∴DG•CE=EF•CD.
∴AB•CE=EF•CD.

∵AD∥BC,
∴四边形ABGD是矩形.
∴AB=DG,AD=BG.
在△CDG中,∠DGC=90°,CD=BC=10,
sinC=
| 4 |
| 5 |
∴AD=BG=4.
∴AD+BC=14.
∴梯形ABCD的面积S=56.
(2)证明:∵DG⊥BC,EF⊥DC,
∴∠DGC=∠EFC=90°.
又∵∠C=∠C,
∴△DGC∽△EFC.
∴DG•CE=EF•CD.
∴AB•CE=EF•CD.
点评:此题考查了梯形的一种常用辅助线-作梯形的高,把梯形分割成直角三角形和矩形,然后解直角三角形求出题目结果.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目

