题目内容
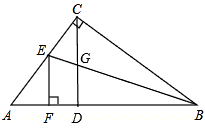
如图,已知在Rt△ABC中,∠ACB=90°,AC=6,BC=8,BE平分∠ABC交AC于点E,EF⊥AB,垂足为F。
(1)求EF的长度;
(2)作CD⊥AB,垂足为D,CD与BE相交于G,试说明:CE=CG;
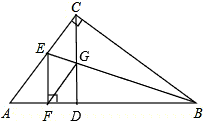
(3)连结FG,试说明:四边形CEFG是菱形。
(1)求EF的长度;
(2)作CD⊥AB,垂足为D,CD与BE相交于G,试说明:CE=CG;
(3)连结FG,试说明:四边形CEFG是菱形。

| 解:(1)∵BE平分∠ABC,∠ACB=90°,EF⊥AB,垂足为F, ∴EF=CE, 在△BFE与△BCE中,∠C=∠BFE=90°, 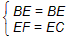 , ,∴△BFE≌△BCE, ∴BF=BC=8, ∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8, ∴AB=10, ∴AF=AB-BF=2, 设EF=x,则CE=x,AE=6-x, 在直角△AEF中,由勾股定理,得AE2=EF2+AF2, ∴(6-x)2=x2+22, 解得x= 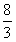 ; ;(2)∵在△BCE中,∠CEB=90°-∠CBE, ∠CGE=∠DGB=90°-∠DBG,∠CBE=∠DBG, ∴∠CEB=∠CGE, ∴CE=CG; |
 |
| (3)∵CD⊥AB,EF⊥AB, ∴CD∥EF, ∵EF=CE,CE=CG, ∴EF=CG, ∴四边形CEFG是平行四边形, 又∵CE=CG, ∴平行四边形CEFG是菱形。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
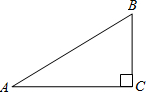 如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
 (2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( )
(2012•驿城区模拟)如图,已知在Rt△ABC中,∠B=90°,D、E分别是边AB、AC的中点,若DE=4,AC=10,则AB的值为( ) 如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长.
如图,已知在Rt△ABC中,∠C=90°,内切圆的半径为3cm,外接圆的半径为12.5cm,求△ABC的三边长. 如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC=
如图,已知在Rt△ABC中,∠C=90°,点D在BC上,AD=BD,sin∠ADC= 如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图:
如图,已知在Rt△ABC中,∠C=90°.根据要求用尺规作图: