题目内容
对于正实数x和y，定义
，那么
- A.“*”符合交换律，但不符合结合律
- B.“*”符合结合律，但不符合交换律
- C.“*”既不符合交换律，也不符合结合律
- D.“*”符合交换律和结合律
D
分析：根据实数混合运算的法则进行计算验证即可．
解答：∵x*y=
，y*x=
=
∴x*y=y*x，故*符合交换律；
∵x*y*z=*z=
=
，
x*（y*z）=x*（
）=
=
∴x*y*z=x*（y*z），*故满足结合律．
∴“*”既符合交换律，也符合结合律．
故选D．
点评：本题考查的是实数的运算，熟知交换律与结合律是解答此题的关键．
分析：根据实数混合运算的法则进行计算验证即可．
解答：∵x*y=
，y*x==∴x*y=y*x，故*符合交换律；
∵x*y*z=
*z==，x*（y*z）=x*（
）==∴x*y*z=x*（y*z），*故满足结合律．
∴“*”既符合交换律，也符合结合律．
故选D．
点评：本题考查的是实数的运算，熟知交换律与结合律是解答此题的关键．
练习册系列答案
相关题目
对于正实数x和y，定义x*y=
，那么（ ）
| x•y |
| x+y |
| A、“*”符合交换律，但不符合结合律 |
| B、“*”符合结合律，但不符合交换律 |
| C、“*”既不符合交换律，也不符合结合律 |
| D、“*”符合交换律和结合律 |
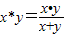，那么（ ）
，那么（ ）