题目内容
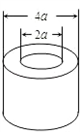
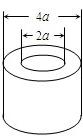如图，空心圆柱底面圆环的外径和内径之比为2：1，若保持内径不变，外径扩大成内径的3倍，则扩大后的空心圆柱的体积是原来的体积的| 8 |
| 3 |
| 8 |
| 3 |
分析：设空心圆柱的内径为2a，则原来外径是4a，变化后的外径是6a，圆柱的高为h，就可以分别表示出变化前后的体积，从而可以求出变化后的体积是原来体积的倍数．
解答：解：设空心圆柱的内径为2a，则原来外径是4a，变化后的外径是6a，圆柱的高为h，
∴变化前的空心圆柱的体积为：π[（2a）2-a2]h=3πa2h，
变化后的空心圆柱的体积为：π[（3a）2-a2]h=8πa2h，
∴扩大后的空心圆柱的体积是原来的体积的倍数是：8πa2h÷3πa2h=
．
故答案为：
．
∴变化前的空心圆柱的体积为：π[（2a）2-a2]h=3πa2h，
变化后的空心圆柱的体积为：π[（3a）2-a2]h=8πa2h，
∴扩大后的空心圆柱的体积是原来的体积的倍数是：8πa2h÷3πa2h=
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
点评：本题是一道图形形积变化的数学题，考查了圆柱体的体积的计算，难度不大，正确运用体积公式就可以了．
练习册系列答案
相关题目
