题目内容
(2012•甘井子区模拟)已知二次函数y=ax2+bx+c中,其函数值y与自变量x之间的部分对应值如表所示:
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,y1与y2的大小关系是
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 4 | 1 | 0 | 1 | 4 | … |
y1<y2
y1<y2
.分析:先设该二次函数的解析式为y=ax2+bx+c(a≠0),把x=0时y=4;x=1时y=1;x=2时y=0代入函数解析式,求出a、b、c的值,进而得出抛物线的解析式,再根据抛物线的对称轴方程求出其对称轴,根据二次函数的增减性即可判断出y1与y2的大小关系.
解答:解:设该二次函数的解析式为y=ax2+bx+c(a≠0),
∵x=0时y=4;x=1时y=1;x=2时y=0,
∴
,
解得,
,
∴此抛物线的解析式为:y=x2-4x+4,
∴抛物线开口向上,对称轴x=-
=2,
∴可知抛物线顶点为(2,0),
∵1<x1<2,3<x2<4,
∴y1<y2.
故答案为:y1<y2.
∵x=0时y=4;x=1时y=1;x=2时y=0,
∴
|
解得,
|
∴此抛物线的解析式为:y=x2-4x+4,
∴抛物线开口向上,对称轴x=-
| -4 |
| 2 |
∴可知抛物线顶点为(2,0),
∵1<x1<2,3<x2<4,
∴y1<y2.
故答案为:y1<y2.
点评:本题考查的是二次函数的性质及用待定系数法求二次函数的解析式,根据题意求出二次函数的解析式及对称轴方程是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
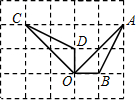 (2012•甘井子区模拟)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为
(2012•甘井子区模拟)如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为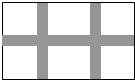 (2012•甘井子区模拟)学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为
(2012•甘井子区模拟)学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为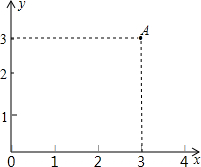 (2012•甘井子区模拟)如图,点A的坐标是( )
(2012•甘井子区模拟)如图,点A的坐标是( )