题目内容
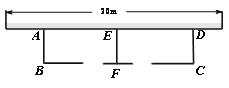
【题目】如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x米。
(1)若两个鸡场总面积为96m2,求x;
(2)若两个鸡场的面积和为S,求S关于x的关系式;
(3)两个鸡场面积和S有最大值吗?若有,最大值是多少?
【答案】(1)8;(2)S=-3x2+36x,(![]() ≤x<12).(3)S最大=108.
≤x<12).(3)S最大=108.
【解析】
试题分析:(1)根据题意可知AD的长度等于BC的长度,列出式子AD-2+3x=34,即可得出用x的代数式表示AD的长,利用题目给出的面积,列出方程式求出x的值;
(2)利用面积公式可得S关于x的关系式;
(3)把代数式表示的面积整理为a(x-h)2+b的形式可求得最大面积,亦可得出AB的长.
试题解析:(1)由题意得:AD=BC,
∵两个鸡场是用34m长的篱笆围成,
∴AD-2+3x=34,
即AD=36-3x,
∵两个鸡场总面积为96m2,
∴列出方程式:x(36-3x)=96,
解得:x=4或x=8,
当x=4时,AD=24>20,不合题意,舍去;
当x=8时,AD=12<20,满足题意,
故x=8时,两个鸡场总面积为96m2;
(2)S=AD×AB=(36-3x)x=-3x2+36x,
∵0<AD≤20,
∴![]() ≤x<12,
≤x<12,
故S关于x的关系式:S=-3x2+36x,(![]() ≤x<12).
≤x<12).
(3)鸡场面积S=x(36-3x)=-3x2+36x=-3(x-6)2+108,
当x=6时,S取最大值108,
此时AD=18<20,符合题意,
即AB=6时,S最大=108.

练习册系列答案
相关题目