题目内容
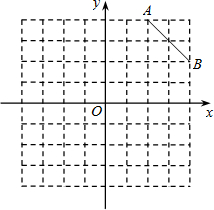 (2012•镇江模拟)在8×8的正方形网格中建立如图所示坐标系,已知A(2,4),B(4,2).
(2012•镇江模拟)在8×8的正方形网格中建立如图所示坐标系,已知A(2,4),B(4,2).(1)在第一象限内标出一个格点C,使得点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
(2)填空:C点的坐标是
(1,1)
(1,1)
,△ABC的面积是4
4
;(3)请探究:在x轴上是否存在这样的点P,使以点A、B、P为顶点的三角形的面积等于△ABC的面积?若存在,请直接写出点P的坐标(可以在网格外);若不存在,说明理由.
分析:(1)此点应在AB的垂直平分线上,在第一象限,腰长又是无理数,只有是点(1,1);
(2)从A,B向x轴引垂线,把所求的三角形的面积分为一个直角三角形ACD和一个直角梯形ABED的面积和减去一个直角三角形BCE的面积;
(3)根据三角形的性质,结合(2)中的方法解答.
(2)从A,B向x轴引垂线,把所求的三角形的面积分为一个直角三角形ACD和一个直角梯形ABED的面积和减去一个直角三角形BCE的面积;
(3)根据三角形的性质,结合(2)中的方法解答.
解答:解:(1)如图所示:
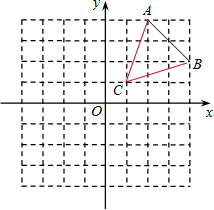
 (2)S△ABC=(1+3)×2×
(2)S△ABC=(1+3)×2×
+
×1×3-
×1×3
=4+1.5-1.5
=4;
C的坐标(1,1),△ABC的面积是4;
故答案为:(1,1),4;
(3)点P的坐标为P(2,0)或(10,0)(2分)

 (2)S△ABC=(1+3)×2×
(2)S△ABC=(1+3)×2×| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4+1.5-1.5
=4;
C的坐标(1,1),△ABC的面积是4;
故答案为:(1,1),4;
(3)点P的坐标为P(2,0)或(10,0)(2分)
点评:此题考查了勾股定理,坐标与图形性质,三角形的面积公式,以及等腰三角形的性质,熟练掌握定理及性质是解本题的关键.

练习册系列答案
相关题目
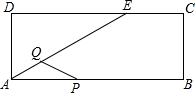 动点Q也从点A出发以每秒1cm的速度向终点E运动.设运动的时间为t秒.解答下列问题:
动点Q也从点A出发以每秒1cm的速度向终点E运动.设运动的时间为t秒.解答下列问题: