题目内容
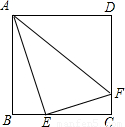
（2005•太原）如图所示，在4×4的正方形网格中，每个小正方形的边长都是1，线段AB和CD分别是图中1×3两个矩形的对角线，显然AB∥CD，请你用类似的方法画出过E点且垂直于AB的直线，并证明．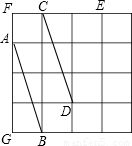
【答案】分析：利用网格来作图，连接AE即可．证明的时候利用勾股定理，求出三角形三边的长，再利用勾股定理证明它是直角三角形．
解答：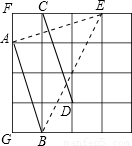
解：答案不唯一，如连接BE．
证明：由网格的特性，得∠F=∠G=∠BAE=90°，
由勾股定理，得AE2=10，AB2=10，BE2=20，
∴AE2+AB2=BE2．
∴∠BAE=90°，
∴EA⊥AB．
点评：本题主要考查了综合利用网格和勾股定理的知识．
解答：
解：答案不唯一，如连接BE．证明：由网格的特性，得∠F=∠G=∠BAE=90°，
由勾股定理，得AE2=10，AB2=10，BE2=20，
∴AE2+AB2=BE2．
∴∠BAE=90°，
∴EA⊥AB．
点评：本题主要考查了综合利用网格和勾股定理的知识．
练习册系列答案
相关题目
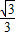x+2与y轴交于点A，与x轴交于点B，⊙C是△ABO的外接圆（O为坐标原点），∠BAO的平分线交⊙C于点D，连接BD、OD．
