题目内容
（2012•威海）探索发现
已知：在梯形ABCD中，CD∥AB，AD，BC的延长线相交于点E，AC，BD相交于点O，连接EO并延长交AB于点M，交CD于点N．
（1）如图①，如果AD=BC，求证：直线EM是线段AB的垂直平分线．
（2）如图②，如果AD≠BC，那么线段AM与BM是否相等？请说明理由．
学以致用
仅用直尺（没有刻度），试作出图③中的矩形ABCD的一条对称轴．（写出作图步骤，保留作图痕迹）
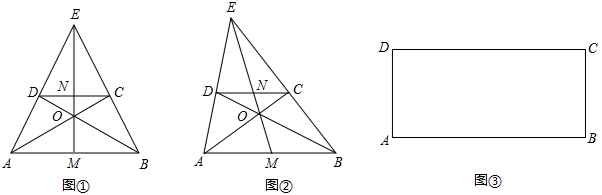
已知：在梯形ABCD中，CD∥AB，AD，BC的延长线相交于点E，AC，BD相交于点O，连接EO并延长交AB于点M，交CD于点N．
（1）如图①，如果AD=BC，求证：直线EM是线段AB的垂直平分线．
（2）如图②，如果AD≠BC，那么线段AM与BM是否相等？请说明理由．
学以致用
仅用直尺（没有刻度），试作出图③中的矩形ABCD的一条对称轴．（写出作图步骤，保留作图痕迹）
分析：（1）AD=BC，CD∥AB，则四边形ABCD是等腰梯形，根据等腰梯形的性质可以得到∠DAB=∠CBA，则AE=BE，即E在AB的垂直平分线上，然后根据OA=OB即可证明O在AB的垂直平分线上，从而证得EM是AB的垂直平分线；
（2）易证△DEN∽△AEM，△OND∽△OMB，则依据相似三角形的对应边的比相等，可以证得：
=
，从而证得BM=AM；
（3）根据（2）可以得到：连接AC，BD，两线交于点O1，矩形ABCD外任取一点E，连接EA，EB，分别交DC于点G，H，即可作出AB的中点M，则直线MO1即为所求．
（2）易证△DEN∽△AEM，△OND∽△OMB，则依据相似三角形的对应边的比相等，可以证得：
| DN |
| BM |
| DN |
| AM |
（3）根据（2）可以得到：连接AC，BD，两线交于点O1，矩形ABCD外任取一点E，连接EA，EB，分别交DC于点G，H，即可作出AB的中点M，则直线MO1即为所求．
解答：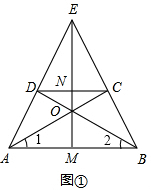
（1）证明：∵AD=BC，CD∥AB．
∴四边形ABCD是等腰梯形，
∴AC=BD，∠DAB=∠CBA，
∴AE=BE
∴点E在线段AB的垂直平分线上，
在△ABD与△BAC中，AB=BA，AD=BC，BD=AC，
∴△ABD≌△BAC，
∴∠1=∠2
∴OA=OB，
∴点O在线段AB的垂直平分线上，
则直线EM是线段AB的垂直平分线；
（2）解：相等．理由：
∵CD∥AB，∴∠3=∠EAB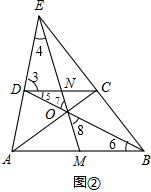
∵∠4=∠4，
∴△DEN∽△AEM
∴
=
，同理
=
∴
=
∵CD∥AB，
∴∠5=∠6
又∵∠7=∠8，
∴△OND∽△OMB
∴
=
，同理
=
∴
=
∴
=
∴AM=BM；
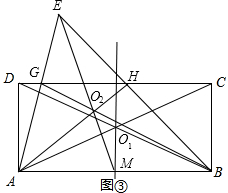
（3）解：作法：如图③①连接AC，BD，两线交于点O1
②在矩形ABCD外任取一点E，连接EA，EB，分别交DC于点G，H
③连接BG，AH，两线交于点O2．
④作直线EO2，交AB于点M．
⑤作直线MO1．
∴直线MO1就是矩形ABCD的一条对称轴．
（1）证明：∵AD=BC，CD∥AB．∴四边形ABCD是等腰梯形，
∴AC=BD，∠DAB=∠CBA，
∴AE=BE
∴点E在线段AB的垂直平分线上，
在△ABD与△BAC中，AB=BA，AD=BC，BD=AC，
∴△ABD≌△BAC，
∴∠1=∠2
∴OA=OB，
∴点O在线段AB的垂直平分线上，
则直线EM是线段AB的垂直平分线；
（2）解：相等．理由：
∵CD∥AB，∴∠3=∠EAB
∵∠4=∠4，
∴△DEN∽△AEM
∴
| DN |
| AM |
| DE |
| AE |
| DE |
| AE |
| DC |
| AB |
∴
| DN |
| AM |
| DC |
| AB |
∵CD∥AB，
∴∠5=∠6
又∵∠7=∠8，
∴△OND∽△OMB
∴
| DN |
| BM |
| OD |
| OB |
| OD |
| OB |
| DC |
| AB |
∴
| DN |
| BM |
| DC |
| AB |
∴
| DN |
| BM |
| DN |
| AM |
∴AM=BM；（3）解：作法：如图③①连接AC，BD，两线交于点O1
②在矩形ABCD外任取一点E，连接EA，EB，分别交DC于点G，H
③连接BG，AH，两线交于点O2．
④作直线EO2，交AB于点M．
⑤作直线MO1．
∴直线MO1就是矩形ABCD的一条对称轴．
点评：本题考查了相似三角形的判定与性质，正确根据相似三角形的对应边的比相等，通过等量代换得到
=
是关键．
| DN |
| BM |
| DN |
| AM |
练习册系列答案
直通贵州名校周测月考直通名校系列答案
培优三好生系列答案
相关题目
（2012•威海）如图，在?ABCD中，AE，CF分别是∠BAD和∠BCD的平分线，添加一个条件，仍无法判断四边形AECF为菱形的是（ ）