题目内容
 实验显示:某种药物在释放过程中,血液中每毫升的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t成反比例.据图中提供的信息,解答下列问题:
实验显示:某种药物在释放过程中,血液中每毫升的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t成反比例.据图中提供的信息,解答下列问题:(1)写出从药物释放开始,y与t之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当血液中每毫升的含药量降低到0.3毫克以下时,药效将明显降低,那么从药物释放开始,至少需要经过多少小时后,药效将明显降低?
(3)当血液中每毫升的含药量y达到0.75毫克时药物才明显有效,问药物的明显有效时间为多少?
考点:反比例函数的应用
专题:溶液问题,待定系数法
分析:(1)首先根据题意,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=
(a为常数),将数据代入用待定系数法可得反比例函数的关系式;
(2)根据(1)中的关系式列不等式,进一步求解可得答案.
(3)把y=0.75代入两个函数求得x值相减即可求得有效时间.
| a |
| t |
(2)根据(1)中的关系式列不等式,进一步求解可得答案.
(3)把y=0.75代入两个函数求得x值相减即可求得有效时间.
解答:解:(1)将点P(3,
)代入函数关系式y=
,
解得a=
,有y=
,
将y=1代入y=
,得t=
,
所以所求反比例函数关系式为y=
(t≥
),
再将(
,1)代入y=kt,得k=
,
所以所求正比例函数关系式为y=
t(0≤t≤
).
(2)解不等式
<0.3,
解得t>5,
所以至少需要经过5小时后,药效将明显降低.
(3)把y=0.75代入到y=
和y=
t,
解得:t=2和t=1.125,
∴药物的明显有效时间为:2-1.125=0.875小时.
| 1 |
| 2 |
| a |
| t |
解得a=
| 3 |
| 2 |
| 3 |
| 2t |
将y=1代入y=
| 3 |
| 2t |
| 3 |
| 2 |
所以所求反比例函数关系式为y=
| 3 |
| 2t |
| 3 |
| 2 |
再将(
| 3 |
| 2 |
| 2 |
| 3 |
所以所求正比例函数关系式为y=
| 2 |
| 3 |
| 3 |
| 2 |
(2)解不等式
| 3 |
| 2t |
解得t>5,
所以至少需要经过5小时后,药效将明显降低.
(3)把y=0.75代入到y=
| 3 |
| 2t |
| 2 |
| 3 |
解得:t=2和t=1.125,
∴药物的明显有效时间为:2-1.125=0.875小时.
点评:本题考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
相关题目
 已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C,直线y=kx+m(k≠0)经过点C、B,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-2,0)、B(x1,0),1<x1<2,与y轴正半轴的交点在(0,2)的上方,顶点为C,直线y=kx+m(k≠0)经过点C、B,下列结论: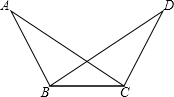 如图,∠ABC=∠DCB,∠ABD=∠DCA,那么AB=CD吗?为什么?
如图,∠ABC=∠DCB,∠ABD=∠DCA,那么AB=CD吗?为什么?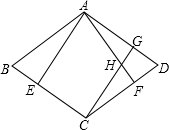 如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF
如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且CE=CF 完成下列推理过程.已知:如图AD⊥BC,EF⊥BC,∠1=∠2,求证:DG∥AB.
完成下列推理过程.已知:如图AD⊥BC,EF⊥BC,∠1=∠2,求证:DG∥AB. 如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE.
如图,在△ABC中,∠ABC=90,过点B作三角形ABC的AC边上的高BD,过D点作三角形ABD的AB边上的高DE. 如图,AB∥CD,∠1=50°,∠2=110°,求∠3的度数.
如图,AB∥CD,∠1=50°,∠2=110°,求∠3的度数.