题目内容
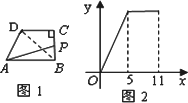
如图11,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°. 设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行.
(1) 当点P在AB边上时,在图中画出一个符合条件的△PQR (不必说明画法);
(2) 当点P在BC边或CD边上时,求BP的长.
 |
(1) 如图.(注:答案不唯一,在图中画出符合条件的图形即可)········ 2分
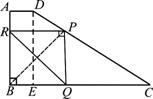
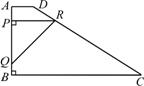 (2) ① 当P在CD边上时,
(2) ① 当P在CD边上时,
由题意,PR∥BC,设PR=x.
可证四边形PRBQ是正方形,∴ PR=PQ=BQ=x.
过D点作DE∥AB,交BC于E,易证四边形ABED是矩形.
∴ AD=BE=1,AB=DE=3.··············· 3分
 又 PQ∥DE,∴△CPQ∽△CDE,
又 PQ∥DE,∴△CPQ∽△CDE,![]() .
.
∴ ![]() ,·················· 4分
,·················· 4分
∴ x=![]() ,即BP=
,即BP=![]()
![]() . ·············· 5分
. ·············· 5分
 (注:此时,由于∠C≠45°,因此斜边RQ不可能平行于BC. 在答题中未考虑此问题者不扣分.)
(注:此时,由于∠C≠45°,因此斜边RQ不可能平行于BC. 在答题中未考虑此问题者不扣分.)
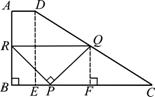
② 当P在BC边上,依题意可知PQ∥BC.
过Q作QF⊥BC,易证△BRP≌△FQP,则PB=PF.····· 6分
易证四边形BFQR是矩形,
设BP=x,则BP=BR=QF=PF=x,BF=RQ=2x.········ 8分
∵ QF∥DE,∴ △CQF∽△CDE,∴ ![]() .············· 8分
.············· 8分
∴ ![]() ,∴ x=
,∴ x=![]() .······················ 10分
.······················ 10分
(注:此时,直角边不可能与两底平行. 在答题中未考虑此问题者不扣分.

练习册系列答案
相关题目