题目内容
如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为30°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从30°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.
[结果精确到0.1米,参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,
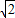 ≈1.41].
≈1.41].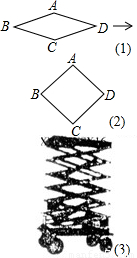
【答案】分析:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于O,则利用菱形的对角线互相垂直可得出对角线AC的长度,继而可得出整个平台的高度.
(2)结合(1)的求解方法可求出此时的平台高度,两者相减即可得出答案.
解答: 解:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于点O,
解:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于点O,
在△ABO中,∠AOB=90°,∠ABO= ∠ABC=15°,
∠ABC=15°,
∴OA=AB•sin∠ABO=1×sin15°≈0.26,
此时AC=2AO≈2×0.26=0.52,
故可得整个装修平台的高度=0.52×6=3.12;
(2)当∠ABC从30°变为90°时,AC=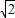 =1.41,
=1.41,
此时的整个装修平台的高度=1.41×6=8.46,
整个装修平台升高了多少米8.46-3.12=5.3米.
点评:此题考查了菱形的性质及勾股定理的知识,解答本题关键是掌握菱形的对角线互相平分且垂直,难度一般.
(2)结合(1)的求解方法可求出此时的平台高度,两者相减即可得出答案.
解答:
 解:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于点O,
解:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于点O,在△ABO中,∠AOB=90°,∠ABO=
 ∠ABC=15°,
∠ABC=15°,∴OA=AB•sin∠ABO=1×sin15°≈0.26,
此时AC=2AO≈2×0.26=0.52,
故可得整个装修平台的高度=0.52×6=3.12;
(2)当∠ABC从30°变为90°时,AC=
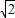 =1.41,
=1.41,此时的整个装修平台的高度=1.41×6=8.46,
整个装修平台升高了多少米8.46-3.12=5.3米.
点评:此题考查了菱形的性质及勾股定理的知识,解答本题关键是掌握菱形的对角线互相平分且垂直,难度一般.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
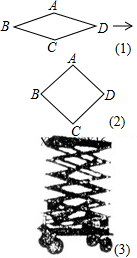 (2011•朝阳)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(2011•朝阳)如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.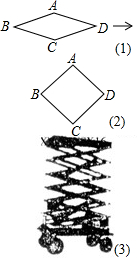 如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
如图(3)是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度. ≈1.41].
≈1.41]. ≈1.41].
≈1.41].
 ≈1.41].
≈1.41].