题目内容
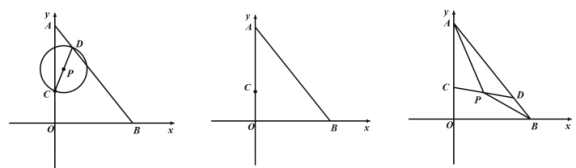
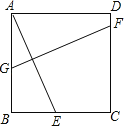
【题目】如图所示,正方形ABCD中,E为BC边上一点,连接AE,作AE的垂直平分线交AB于G,交CD于F,若BG=2BE,则DF:CF的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
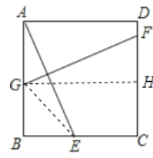
过点G作GH⊥CD于H,连接GE,可证△ABE≌△GHF,设BE=HF=x,通过BG=2BE,得到BG=2x,从而得到AG=GE=![]() ,然后再通过线段相等的关系得到DF和FC的长,即可得到答案.
,然后再通过线段相等的关系得到DF和FC的长,即可得到答案.
解:过点G作GH⊥CD于H,连接GE,则∠GHF=90°,即四边形AGHD为矩形,四边形BCHG为矩形,CH=BG,
∵GF垂直平分AE,四边形ABCD是正方形,
∴∠ABE=∠GHF=90°AB=AD=GH,AG=GE,
∵∠BAE+∠AGF=90°,∠AGF+∠FGH=90°,
∴∠BAE=∠FGH,
∴△ABE≌△GHF,
∴BE=HF,
设BE= HF =x,
∵BG=2BE,
∴BG=2x,即HC=2x,
∴FC=3x,
在直角三角形GBE中,![]() ,
,
∴AG=HD=![]() ,
,
DF=HD-HF=![]() ,
,
∴![]() ,
,
故选:A.

练习册系列答案
相关题目