题目内容
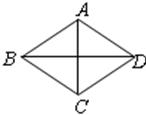
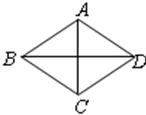
在菱形ABCD中，两条对角线AC=6，BD=8，则此菱形的边长为（ ）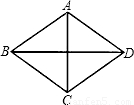
A．5
B．6
C．8
D．10
【答案】分析：根据菱形对角线互相垂直平分的性质，即可求AO，BO，根据勾股定理即可求AB的值，即菱形的边长．
解答：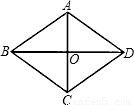
解：∵菱形对角线互相垂直平分
∴△AOB为直角三角形，且AC=2AO，BD=2BO，
∴AO=3，BO=4，
∴AB=
=5，
故选 A．
点评：本题考查了菱形对角线互相垂直平分的性质，考查了勾股定理在直角三角形中的运用，本题中根据勾股定理求AB的值是解题的关键．
解答：
解：∵菱形对角线互相垂直平分∴△AOB为直角三角形，且AC=2AO，BD=2BO，
∴AO=3，BO=4，
∴AB=
=5，故选 A．
点评：本题考查了菱形对角线互相垂直平分的性质，考查了勾股定理在直角三角形中的运用，本题中根据勾股定理求AB的值是解题的关键．
练习册系列答案
相关题目
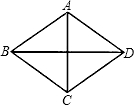在菱形ABCD中，两条对角线AC=6，BD=8，则此菱形的边长为（ ）| A、5 | B、6 | C、8 | D、10 |
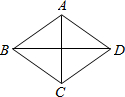（2012•路南区一模）如图，在菱形ABCD中，两条对角线AC=12，BD=16，则此菱形的边长为（ ）
