题目内容
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
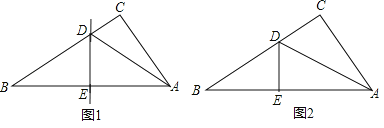
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
【答案】(1)CD= ![]() ;(2)CD= 3
;(2)CD= 3
【解析】试题分析:(1)利用对称找准相等的量:BD=AD,∠BAD=∠B,然后利用周长求得答案;
(2)利用折叠找着AC=AE,利用勾股定理列式求出AB,设CD=x,表示出BD,AE,在Rt△BDE中,利用勾股定理可得答案.
试题解析:(1)由折叠可知,AD=BD,设CD=x,则AD=BD=8-x,
∵∠C=90°,AC=6,
∴62+x2=(8-x)2,
∴x=![]()
∴CD=![]()
(2)在Rt△ABC中,AC=6,BC=8,∴AB=![]() =10,
=10,
由折叠可知,AE=AC=6,CD=ED,∠ADE=∠C=90°,
∴BE=10-6=4,设CD=x,则DE=x,BD=8-x,
∴x2+42=(8-x)2,
∴x= 3,
∴CD= 3

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目